Les constructions
animées
Lorenzo Mascheroni
(1750-1800) démontrait dans son livre 'Géométrie
du compas' édité en 1797 que
'Tout
ce qui peut être construit avec la règle et le compas
peut l'être avec le seul compas."
Ce livre était dédicacé à Napoléon.
D'ailleurs, la construction permettant de retrouver le centre perdu
d'un cercle a gardé le nom de 'problème de Napoléon'.
En savoir plus ICI :
http://fr.wikipedia.org/wiki/Lorenzo_Mascheroni#.C5.92uvres_math.C3.A9matiques
Je vous propose
ci-dessous quelques constructions animées plus ou moins faciles.
Dans le
menu, les astérisques indiquent le degré de difficulté
de chaque construction.
Plus il y en a, plus les constructions sont délicates.
Choisir sa construction puis cliquer GO.
Les boutons permettent de stopper ou de poursuivre la construction
à tout instant.
Quelques explications pour
les plus faciles
.Triangle
équilatéral
On construit trois côtés de même
longueur : AB = AC = BC.
Le triangle ABC est donc équilatéral.
***********************************
|
|
.Hexagone
régulier
Nous construisons six triangles équiltéraux
ABC, ACD, ADE, AEF, AFG et AGB.
La mesure de la longueur commune de tous les côtés
est AB qui est le rayon du cercle initial.
Il s'ensuit que BCDEFG est un hexagone régulier.
En chacun des sommets, l'angle mesure 120° (c'est
à dire deux fois 60°).
***********************************
|
|
.Quatrième
sommet D du parallélogramme
Nous avons construit ici, un quadrilatère ayant
ses côtés opposés de même
longueur.
Nous construisons : AD = BC et DC = AB.
ABCD
est donc un parallélogramme.
.Parallèle
à une droite (AB) passant par un point C
Nous construisons selon la méthode précédente
un parallélogramme.
Le
résultat découle de la propriété
du parallélogramme :
c'est un quadrilatère qui a ses côtés
opposés parallèles.
***********************************
|
|
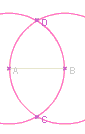
.Médiatrice
du segment [AB]
La médiatrice de [AB] est l'ensemble des
points équidistants des extrémités
A et B.
Nous avons cosntruit C équidistant de A et
de B, puis
D équidistant de A et de B.
Notons
que la médiatrice de [AB] est aussi l'axe de
symétrie de [AB].
Remarque
:
Pour accélérer le tracé, nous
avons gardé une distance commune égale
à AB pour C et D. Ici, deux cercles ont suffi.
Ce n'est pas obligatoire.
On
peut changer l'écartement du compas entre les
points C et D (en haut et en bas).
***********************************
|
|
.Bissectrice
d'un angle
Entre autres définitions, la bissectrice
d'un angle est l'axe de symétrie de cet angle.
Ici nous avons choisi un triangle AOB isocèle.
La bissectrice de l'angle en A est dons aussi l'axe
de symétrie de [AB].
Il suffit donc de construire la médiatrice
de[AB].
A étant sur cette bissectrice, il suffit de
construire un seul point I équidistant
de A et B.
***********************************
|
|
.Symétrique
M'd'un point M par rapport à la droite (AB)
Les
deux cercles centrés en A et B ont chacun (AB)
comme axe de symétrie.
Leurs intersections M et M' sont donc symétriques
par rapport à (AB).
***********************************
|
|
.Symétrique
A' de A par rapport à B
Dans le demi hexagone régulier construit
avec le cercle de centre B et de rayon BA,
nous avons AB = BA'
***********************************
|
|
|
.Tangente
(CD) en un point A du cercle de centre O
La tangente en un point A du cercle est perpendiculaire
au rayon OA qui aboutit en A.
Si B est le symétrique de O par rapport à
A, alors la tangente est la médiatrice de [BO].
Ici on a donc construit la médiatrice (CD) de
[OB]
***********************************
|
|
|
Quelques démonstrations
plus délicates
MILIEU
d'un SEGMENT
 |
Pour la démonstration, utilisons
A" symétrique de A' par rapport à
A' et H intersection de (EF) et (AA").
Par construction A' est le symétrique de B par rapport
à A (Voir constructions précédentes)
et on a AA" = 2 AA' soit
AA" = 4 AB.
E et F sont symétriques par rapport à (AB) et
donc (EF) est perpendiculaire à (AB).
Dans le cercle de centre E passant par A et I, (EF)
et donc (EH) est perpendiculaire à la corde [AI].
On sait que tout diamètre perpendiculaire
à une corde est médiatrice de cette corde.
(EF) est donc médiatrice de [AI] et H est le milieu
de [AI]. |
Nous allons montrer que AH = AB/4 ce qui nous mènera
à la conclusion I milieu de [AB].
Dans le triangle rectangle AEA" ( inscrit dans
un demi cercle ), nous avons la relation (
H pied de la hauteur issue de E ) :
EA² = AA"" x AH soit
EA² = 4 AB x AH mais EA = AB (cercle
de centre A passant par B et E)
d'où
AB² = 4
AB x AH
donc AB = 4 AH
et finalement AH = AB / 4 et alors AI = AB /2
puisque AI = 2 AH.
***********************************
TANGENTE
en un point M extérieur au cercle
 |
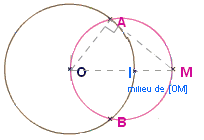Les
deux tangentes issues de M sont symétriques par rapport
à la droite (OM).
Une fois A construit, le point B est obtenu par la symétrie
d'axe (OM).
Si A est le point de contact de l'une des tangentes, la tangente
(MA) est perpendiculaire en A au rayon [OA] du cercle de centre
O.
Il suffit donc de tracer le cercle de centre le milieu I de
[OM] car le triangle OAM inscrit dans un demi cercle est rectangle.
Le milieu I de [OM] est construit avec la procédure vue
précédemment.
|
***********************************
Compléter
un carré BADC connaissant les sommets B et A
***********************************
INTERSECTION
de deux droites PERPENDICULAIRES
 |
On construit A' symétrique de A par rapport à
(CD).
(CD) est donc la médiatrice de [AA'].
L'intersection
I de (AB) et (CD) est donc le point d'intersection de
la médiatrice de [AA'] et de (CD).
I le milieu de [AA'] que nous construisons par
la méthode vue ci-dessus.
|
***********************************
Le
CENTRE perdu d'un CERCLE, problème de NAPOLEON
|
Pour
la démonstration, utilisons les points A' et A"
de la figure (intersections de (AD) avec les cercles jaunes
et noirs).
Posons R le rayon du cercle noir dont on cherche
le centre.
Posons r = AB = AC ,
rayon de chacun des cercles verts.
Soit
H'' l'intersection de
(EF) avec (AA').
Soit H' l'intersection de (BC) avec (AA').
 |
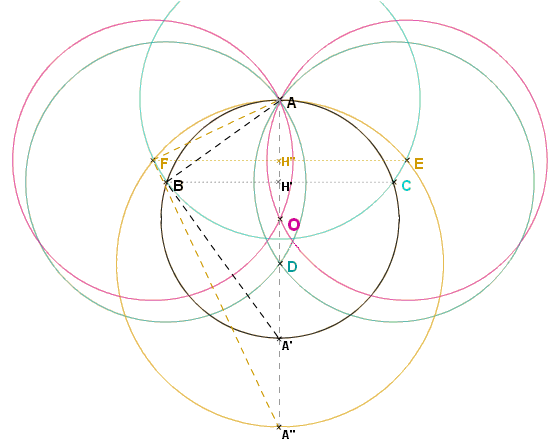Le
quadrilatère ABDC est un losange
car
BA = BD dans le cercle vert de centre
B
et
CA = CD dans le cercle vert de centre
C
et
BA = CA = r dans le cercle vert de centre
A
On en déduit que ses diagonales sont perpendiculaires
et se coupent en leur milieu donc AH'
= AD / 2 .
Le quadrilatère AEOF est un losange
car
EA = EO dans le cercle rose de centre
E
et
FA = FO dans le cercle rose de centre
F
et
pour raison de symétrie (grâce
à AB=AC),
EA = FA .
On en déduit que ses diagonales sont perpendiculaires
et se coupent en leur milieu donc AH''
= AO / 2 .
Nous
allons montrer que AO = R = OA', ce qui prouvera que O
est bien le centre du cercle noir initial.
|
|
Le
triangle AFA"
est rectangle car inscrit dans le demi cercle jaune
de centre D.
Dans ce triangle rectangle, on a la relation
AF² = AH''
x AA" soit r² = AH''
x 2AD.
Alors AH''
= r² / 2 AD
donc
AO / 2 = r² / 2 AD
soit
AO = r² / AD
donc
AD = r² / AO
|
Le
triangle ABA'
est rectangle car inscrit dans le demi cercle noir de
rayon R.
Dans ce triangle rectangle, nous avons la relation
AB² = AH' x AA' soit r² = AH' x 2R.
Alors AH' = r² / 2 R
soit
AD / 2 = r² / 2 R
Donc
AD = r² / R
|
Des
deux relations précédentes notées en vert,
nous déduisons que
r²
/ AO = r² / R
ceci implique AO = R
Comme O est situé sur le diamètre du cercle noir
de rayon R, cela prouve bien que O est le centre de ce cercle.
|
***********************************
INTERSECTION
de deux sécantes NON perpendiculaires
A priori la construction paraît compliquée.
Cependant on réinvestit la construction des symétriques
par rapport à une droite
ainsi que le problème de Napoléon que nous avons étudiés
précédemment.
Nous construisons
successivement,
-les symétriques A' et B' de A et B par rapport à
(CD) puis
-les symétriques C' et D' de C et D par rapport à
(A'B') puis
-les symétriques A" et B" de A' et B' par rapport
à (C'D').
Enfin nous utilisons la procédure de Napoléon pour
déterminer le centre du cercle passant par B, B' et B".
Cette construction utilise points B et B" symétriques
par rapport à (A'B').
Il faut cependant que la distance BB' ne soit ni trop grande ni
trop petite.
En cas de difficutlé il faudra réessayer avec un autre
point de la doite (AB).
Ainsi
-les sécantes non perpendiculaires (AB) et (CD) se coupent
en un point O.
La droite (A'B') symétrique de (AB) par rapport à
(CD) passe aussi par O qui est son propre symétrique (point
invariant).
O est commun à (AB) (CD) et (A'B').
En poursuivant, on trouve que O est commun aux cinq droites
(AB) (CD) (A'B') (C'D') et enfin (A"B").
Dans la
symétrie d'axe (CD) :
A donne A' tel que OA = OA'
B donne B' tel que OB = OB' |
Dans la
symétrie d'axe (A'B') :
C donne C' tel que OC = OC'
D donne D' tel que OD = OD' |
Dans la
symétrie d'axe (C'D') :
A' donne A" tel que OA' = OA"
B' donne B" tel que OB' = OB" |
Finalement OB
= OB' = OB" donc O est le centre du cercle passant
par B, B' et B".
Il en est de même pour les points A, A' et A" que l'on
utilisera si B, B' et B" sont confondus.
Si les doites sont perpendiculaires, choisir la construction vue plus
haut,
car dans cette procédure les points B et B" seront confondus
(de même pour A et A").
***********************************
Milieu
d'un arc de cercle
|
|
Les cercles
roses de centres C et D ont pour
rayon OE
Posons
R le rayon du cercle intial de centre
O.
Posons r = DA = DE = DF = CF =
CB = CE (rayon des cercles
verts).
Par construction
(CD) est axe de symétrie de la figure.
Par construction (IJ) est axe de symétrie de (AB).
Il suffit donc de montrer que
I est sur le cercle de centre O
pour prouver qu'il est le milieu de l'arc.
Idem pour le point J.
-La construction du paralléogramme OABD
implique
OA = DB et comme OA = OB nous aurons
OA = OB = DB
-La construction du parallélogramme OBAC
implique OB = CA
Donc
OA = OB = DB
= CA
Nous avons aussi CO
= AB = OD
|
|
Nous
allons démontrer que OI = R
Dans
le triangle rectangle COI,
CI² = CO² + OI² soit OE² = AB²
+ OI² soit OE² = AB²
+ OI²
Dans le triangle rectangle COE,
OE² = CE² - CO² soit OE²
= r² - AB²
De ces deux relations donnant OE² nous déduisons
AB² + OI² = r² - AB²
soit
r² = 2 AB² + OI²
OBD est un triangle isocèle, sa hauteur est aussi médiane.
Dans le triangle rectangle CHB
CB² = CH² + HB²
CB² = (3/2 AB)² + HB² soit
r² = 9/4 AB² + HB²
Dans le triangle rectangle OHB
OB² = OH² + HB²
OB² = (1/2 AB)² + HB² soit
R² = 1/4 AB² + HB²
Ainsi en rapprochant les deux expressions r²
= 9/4 AB² + HB² et R²
= 1/4 AB² + HB²
nous obtenons
r² - R² = 9/4 AB² - 1/4 AB²
ou
r² - R² = 2
AB²
soit
r² = 2 AB² + R²
En rapprochant
les deux expressions r² =
2 AB² + OI² et r²
= 2 AB² + R²
nous obtenons
R² = OI² soit finalement
OI
= R
C'est bien ce que nous voulions démontrer.
|
***********************************
/
2 et donc AQ = AB
AB