Les constructions
animées
Cette géométrie
à la règle avec une seule unité m'a été
proposée par mon collègue Ruben Rodriguez Herrera.
A l'origine ce serait la "géométrie du petit indien".
Pour en savoir plus, voir "Du dessin perçu à la
figure construite" Editions Ellipses 2005.

Démonstration
de la construction d'une parallèle à une droite passant
par M
en utilisant uniquement la règle avec une seule
unité
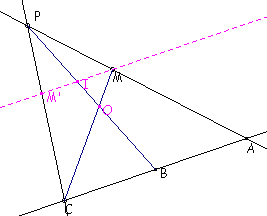
.Soient
les points A et C de la droite initiale.
.B
est sur (AC) tel que B milieu de [AC].
.Choisissons P sur (AM) tel que P ne soit pas sur [AM]
.Soit O à l'intersection de (PB) et (MC)
.Soit (MM') la parallèle à (AC) passant par M.
Nous allons montrer que M' , O et A sont alignés.
Cela justifiera la construction de M' comme
intersection de (PC) et (AO) utilisée dans l'animation précédente.
Considérons l'homothétie de centre P et de rapport
PM / PA, alors
A a pour image M
C a pour image M' et
B milieu de [CA] a pour image I milieu de [M'M].
Les triangles
(MIO) et (CBO) sont homothétiques dans une homothétie
de centre O et de rapport OI/OB (côtés parallèles
deux à deux)
donc OI/OB = MI/BC *
Nous avons M'I /BA = MI/BC
car M'I = MI et BA = BC
Nous déduisons donc de * que
M'I/BA = OI/OB
et comme
(M'I) //(BA)
(IO) // (OB)
Il vient que les triangles (M'IO) et (ABO) sont homothétiques
dans une homothétie de centre O et de rapport OI/OB
Il s'ensuit que les points M', O et A sont alignés.
Ainsi pour construire la parallèle à (AC) passant par
M, il suffit de construire les droites (OA) et (PC).
Leur instersection donne le point M' tel que (MM') //(AC).



|