Le
cône et le cylindre
Pour
chaque animation
CLIQUER l'image puis OUVRIR puis DOUBLE CLIQUER le
fichier .html
A
voir si notre vie
Epouse ou non ta forme
Au long de la durée.
Mais dans quel sens alors ?
Pour toujours s'élargir ?
Pour toujours se fermer ?
... Le cône de Guillevic
Développement
du cône
 CLIQUER
CLIQUER

 Une
coupe de champagne ? Une
coupe de champagne ?
Vous venez de boire une coupe de champagne conique remplie simplement
à mi-hauteur.
Votre ami a complètement rempli et vidé sa coupe (même
forme et même taille).
Quel est le rapport entre la quantité qu'il a bue et celle que
vous avez vous-même bue ?
Deux ?
Non pas du tout ! Attention à l'alcootest c'est Huit !
La perception
de certains rapports d'aires et de volumes est parfois trompeuse.
Le résultat est lié à la théorie des
rapports dans les figures semblables.
Le rapport des aires est alors le carré du rapport des longueurs
et celui des volumes
est le cube du rapport des longueurs.
Nous pouvons penser que le verre plein est un agrandissement du
verre à moitié rempli
avec un rapport égal à 2.
Le rapport des volumes est donc 23 soit 8. |
 |
Quand vous avez
bu la moitié de la coupe de champagne, à quelle hauteur
du verre arrive le champagne restant ?
Le champagne restant arrive à la racine cubique de (1/2) de la
hauteur totale du verre soit environ aux 4/5 èmes
(~0.79) de la hauteur du verre.
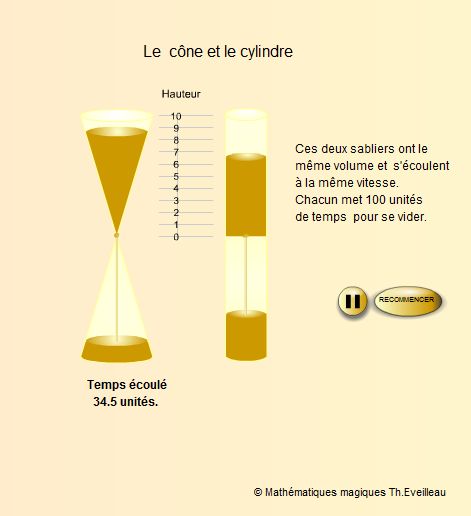
Nous allons simuler
ci-dessous deux sabliers ayant la même contenance, l'un est
conique et l'autre est cylindrique. Ensuite nous suivrons les courbes.
Deux
sabliers : le cône et le cylindre
Dans le cas du
cylindre, le volume est proportionnel à la hauteur du cylindre,
ce n'est absolument pas le cas avec un cône.
Ci-dessous
on peut stopper faire avancer ou redémarrer l'animation.
CLIQUER

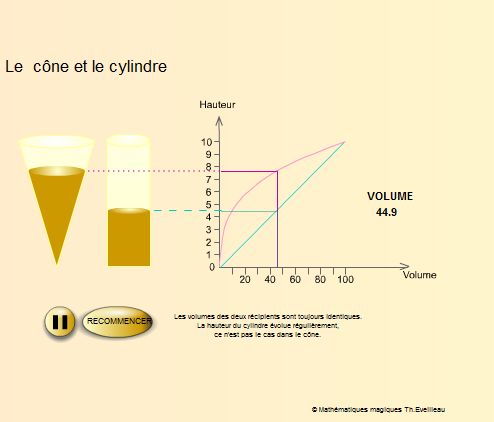
Les courbes comparées
des hauteurs en fonction du volume
La hauteur du cylindre est proportionnelle au volume (droite passanr
O).
La hauteur du cône augmente très vite lorsque le volume
est petit puis elle croît
plus lentement au fur et à mesure que le cône s'élargit
vers le haut.
CLIQUER
Le
volume du cylindre est donné par l'expression suivante fonction
de la hauteur h et du diamètre d du cylindre :
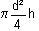 . .
Le
volume du cône est donné par l'expression suivante : . .
Lorsque la hauteur
varie, le diamètre varie et donc également la surface
du disque en haut du cône.
L'aire
et le volume d'une sphère sont ici

Petit
problème
|
Dans
un verre conique, on a versé du mercure, puis de l'eau
et enfin de l'huile de façon
à ce qu'il y ait la même hauteur de chaque produit.
Quel est celui qui pèse le plus lourd : le mercure, l'eau
ou l'huile ?
La densité de l'huile est 0,915 et celle du mercure 13,59.
SOLUTION
Appelons Vm le volume du mercure, Ve
le volume de l'eau et Vh celui
de l'huile.
En utilisant les résultats ci-dessus, nous obtenons
Vm + Ve = 23
Vm soit Vm
+ Ve = 8 Vm
donc Ve = 7 Vm.
Vm + Ve + Vh
= 33 Vm donc Vm
+ 7 Vm + Vh = 27
Vm ce qui donne Vh
= 19 Vm.
Les trois masses sont donc
pour l'eau : 7 Vm
;
pour le mercure : 13,59 Vm
;
et enfin pour l'huile : 0,915 x 19 Vm
soit 17,384 Vm.
dans le verre c'est donc l'huile qui a la masse la plus grande,
puis le mercure puis l'eau.
|
 |

Développement
du cylindre

CLIQUER puis
OUVRIR puis DOUBLE CLIQUER le fichier
|


 Une
coupe de champagne ?
Une
coupe de champagne ? 

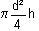 .
.
