Retrouver la formule de l'aire d'un disque connaissant le périmètre

Disquaire

L'intégrale avant l'heure...

Nous avons vu avec Archimède différentes procédures pour retrouver l'aire d'un disque connaissant son périmètre.

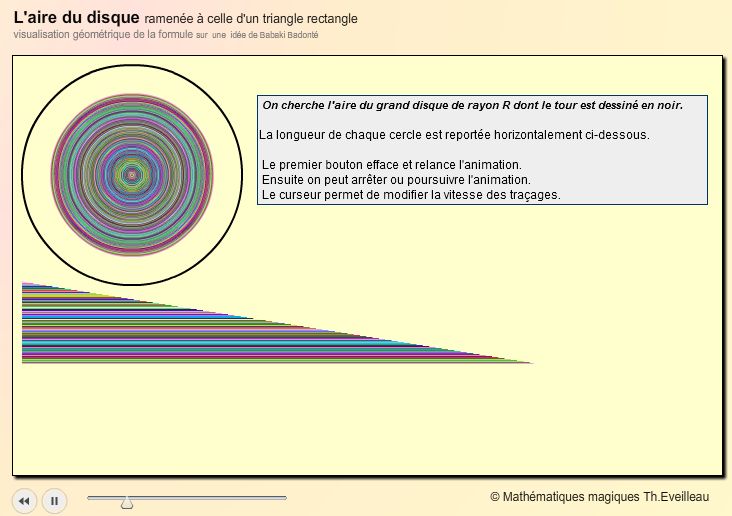
Ci-dessous, je réalise une animation sur une idée que m'a proposée Babaki.
il s'agit de construire un triangle rectangle avec les longueurs des cercles concentriques intérieurs au disque de rayon R.

Archimède brillant ingénieur mais aussi mathématicien, montrait déjà, par une méthode d'exhaustion que :
"tout cercle est équivalent à un triangle rectangle dans lequel
l'un des côtés de l'angle droit est égal au rayon du cercle et la base égale au périmètre du cercle".
Il est d'ailleurs considéré par ses nombreux travaux, comme un initiateur du calcul intégral.

Chaque fois qu'un cercle coloré est dessiné, un segment de même couleur et de longueur égale au périmètre du cercle, est reporté
horizontalement sous le segment précédent.

Nous obtenons ainsi successivement des triangles dont les côtés de l'angle droit mesurent :
- r pour le petit côté
- 2 π r pour le grand côté,
avec r variant de 0 à R, rayon du disque initial.

Notons que tous ces triangles sont semblables car le grand côté de l'angle droit est proportionnel au petit.
Le rapport de proportionnalité est toujours égal à π.

On peut donc considérer que la suite des segments dessinés forme bien un grand triangle
dont les côtés de l'angle droit mesurent R et 2 π R.

Il s'agit en quelque sorte de l'intégrale :

On peut modifier la vitesse du tracé en déplaçant le curseur.
Les autres boutons permettent de Recommencer, Stopper ou Poursuivre.
Les couleurs sont différentes à chaque relance.

CLIQUER

A propos de π avec des images d'Antonio de Garcia de Pablo