Les tétraèdres encreurs, un pavage original avec une pyramide colorée. Le tétraèdre régulier Le tétraèdre formé de triangles isocèles Le tétraèdre quelconque Devenez magicien avec le tétraèdre    tour expliqué Construction d'un tétraèdre adapté à tous les cas   Le tétraèdre régulier Dans l'animation ci-dessous, indiquer si l'on veut ou non une trame de fond. Choisir la trajectoire : lignes, pieuvre ou hexagones. Lancer alors l'animation en cliquant sur le bouton GO. Le tétraèdre va laisser son empreinte et paver le plan en suivant la trajectoire choisie. La pyramide roule sans glisser autour de ses arêtes. Elle peut revenir au point de départ dans sa position initiale, quel que soit le chemin emprunté.   CLIQUER   Devenez magicien Voici à droite, un modèle pour construire rapidement le tétraèdre utilisé dans ce tour. Imprimer ce modèle : clic droit sur l'image, puis clic sur imprimer Découper ce modèle dans du carton léger ou du papier assez solide. Couper bien régulièrement. Replier les triangles blancs pour former un tétraèdre. Faire pénétrer les triangles gris à l'intérieur des arêtes ouvertes. Le solide tient sans colle. Imprimer le réseau coloré ci-dessous : clic droit sur l'image, puis clic sur imprimer. Le tour Prendre le tétraèdre que l'on vient de construire. Placer ce solide sur le triangle noir au sommet du réseau coloré qui a été imprimé. Tournez le dos, et demandez à un ami de faire rouler ce tétraèdre sur le réseau coloré, en le faisant pivoter autour de ses arêtes. L'ami s'arrêtera quand il voudra, et il notera la couleur de la case d'arrivée. Vous lui demandez de compter lentement tout haut jusqu'à dix (juste pour le perturber...). Ensuite il doit glisser, sans rouler, son solide jusqu'au triangle noir de départ (pour que vous ne voyiez pas la case d'arrivée). Vous vous retournez et demandez à toucher la face inférieure. Alors fièrement vous nommez la couleur sur laquelle il s'est arrêté pendant que vous étiez retourné. Voici, juste après le réseau coloré, le secret de ce tour. 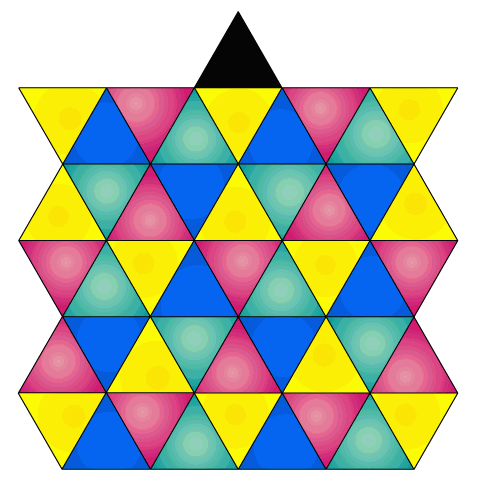Secret du tour Ce tour allie géométrie et truc de joueur de cartes. Pour marquer une carte d'un paquet pendant un "tour" de cartes, il est usuel de déposer un peu de mine de crayon à l'aide d'un doigt sur une des tranches ; cette très légère empreinte peut se confondre avec une tache normale due à un jeu utilisé depuis longtemps. De la même façon, marquez une face du tétraèdre, tout près d'un sommet. Placez alors le tétraèdre, secrètement pipé, sur le triangle noir ; la face marquée est placée contre le réseau, le coin taché tout en haut. C'est la localisation de cette tache à la fin du tour qui vous indiquera la couleur du triangle d'arrivée de votre ami. Il suffit de repérer cette position qui ne peut être que l'une des quatre indiquées. Ce tour est infaillible. Si la tache est à gauche de la face, la case d'arrivée est bleue. Si la tache est à droite de la face, la case d'arrivée est verte. Si la tache est en haut de la face, la case d'arrivée est jaune. Si la tache est invisible donc contre le réseau, la case d'arrivée est rouge. La justification réside dans l'animation précédente. Il suffit d'imaginer un tétraèdre coloré laissant des empreintes comme dans l'animation. Fait important : en revenant sur le triangle noir, le solide ne fait que glisser, on ne change pas la face au sol. La position relative de la marque est constante par rapport aux quatre faces du tétraèdre. Il suffit donc de la déterminer a priori. La position finale de la marque détermine alors celle des autres et notamment celle de la face contre le réseau.   Construction d'un tétraèdre adapté à toutes les formes de triangles Que le tétraèdre soit constitué de triangles équilatéraux, isocèles ou quelconques, les quatre triangles qui le composent sont ici superposables. 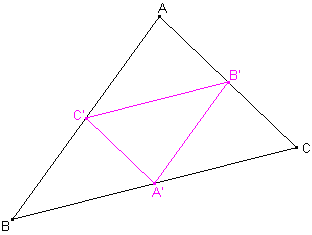Pour le construire simplement : -partir du triangle ABC désiré ; -marquer les milieux A', B' et C' des trois côtés ; -plier sur B'C', B'A' et C'A'. Les trois sommets A, B et C se confondent en un seul sommet A. Les arêtes du tétraèdre sont AC', AB', AA', C'B', A'B', A'C'. La construction n'est possible que si aucun des angles du triangle initial n'est obtus. Dans le cas particulier d'un triangle rectangle, la pyramide s'aplatit en une enveloppe rectangulaire. Lorsque la construction est possible, la pyramide obtenue - a quatre faces superposables ; - les arêtes opposées sont de même mesure ; - les trois droites qui joignent les milieux des arêtes opposées sont concourantes (ce qui vaut pour tout tétraèdre) et deux à deux orthogonales car les parallélogrammes dont elles sont les diagonales sont des losanges (ne pas oublier que les trois sommets A, B et C ne feront qu'un seul sommet A).