La
planche de Galton
 Description
et simulation Description
et simulation
Issu
d'une famille de scientifiques, Francis Galton
(1822-1911) était le cousin de Charles Darwin et voulait justifier
la transmission des possibilités intellectuelles par l'hérédité
pour améliorer l'espèce humaine... Il
s'intéressa à la géographie, la météorologie,
l'anthropologie. Il fut l'un des pionniers
en statistique, dans un but purement utilitaire. Ses travaux dans le
domaine des statistiques restèrent cependant secondaires pour
Galton, à côté de ses études sur l'origine
des espèces. Il créa une planche à deux étages
afin d'étudier les lois du hasard.
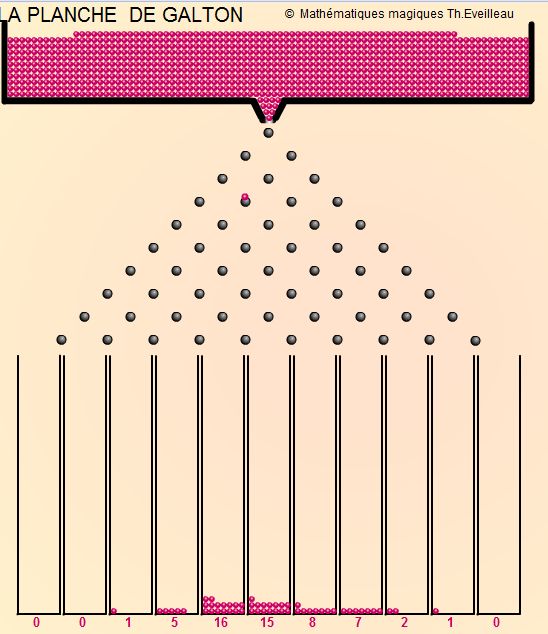
Dans la planche de Galton, plusieurs billes tombent au travers d'une
pyramide de clous sur une planche inclinée. En
bas se trouvent des boîtes dans lesquelles tombent les billes.
La
bille finit sa trajectoire en tombant dans une des boîtes du bas.
On
trouve quelquefois ce jeu dans les foires. L'animateur du stand attribuera-t-il
la même valeur à chaque boîte de la planche ?
Chaque fois qu'une bille tape un clou, elle
a une chance sur deux de tomber d'un côté ou de l'autre.
Elle a donc la même probabilité (p=0.5) de continuer sa
chute à gauche ou à droite. Si
nous réalisons l'expérience un grand nombre de fois (400
fois par exemple), les billes accumulées dans les boîtes
forment ainsi un histogramme.
CLIQUER
 Analyse Analyse
Dans les jeux de hasard on peut
prévoir les résultats pour un très grand nombre
de jeux, mais prévoir le résultat individuel d'un
joueur particulier est tout à fait incertain. Lorsqu'on lance
un dé on a une chance sur six d'obtenir un 4. Cependant si
on lance le dé six fois de suite nous ne sommes pas certains
d'obtenir un 4 au moins une fois... par contre si on le lance 1000
fois on aura plus de chances d'obtenir le 4 une fois sur 6 donc
environ 166 fois.
Avec les lois du chaos, on ne croit pas pouvoir prédire l'ensemble
des phénomènes de l'Univers.
Dans la planche de Galton la probabilité
qu'une bille arrive dans une colonne donnée est égale
au nombre de chemins possibles y aboutissant divisé par le
nombre total de tous les chemins.
Sur la figure ci-dessous, au 6ème niveau la bille
a 10 chances sur 32 d'arriver en A et 10 chances sur 32 d'arriver
en B. Notons que le 6ème
rang, la somme des probabilités
est de 1.
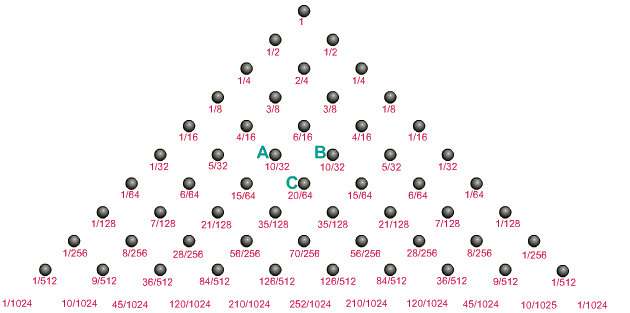
Pour arriver en C au rang suivant, la bille doit passer par A ou par
B. De A elle a une chance sur 2 d'arriver en C, de B elle a aussi
une chance sur 2 d'arriver en C. Nous obtenons alors elle a donc une
probailité de (01/2)(10/32) + (1/2)(10/32))=
20/64.
Nous retrouvons aux numérateurs des fractions, des nombres
qui rappellent ceux que nous avions dans le triangle de Pascal : ce
sont les coefficients du binôme de Newton.
Avec un très grand nombre de billes et un très grand
nombre de clous, la courbe de répartition des billes dans les
différentes boîtes donne une courbe en cloche. Cela résulte
de la loi de Gauss : lorsque le nombre de billes lâchées
tend vers l'infini ainsi que le nombre de clous, la courbe de leur
répartition dans les différentes boîtes se stabilise
pour donner la courbe de Gauss (courbe en cloche répartition
normale aléatoire).
Voir la démonstration ici : http://fr.wikipedia.org/wiki/Loi_binomiale
Devinette
David vient de lancer sa pièce 50 fois de suite. Elle est retombée
50 fois sur Face. Quelle chance a-t-il de la voir retomber sur Pile
la 51ème fois ?
Réponse...
Certainement aucune ! En effet si elle est tombée tant de fois
de suite sur Face, c'est qu'elle est truquée : les 2 côtés
sont sûrement identiques ;o).
|