Les chemins de Pascal Visualiser les chemins Dénombrement des chemins Le triangle de pascal Les abeilles Les rectangles   Cf aussi le jeu

Visualiser les chemins

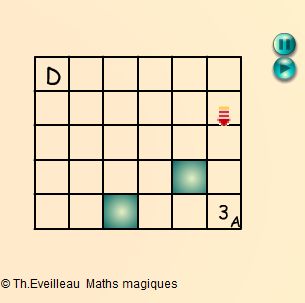
Nous voulons nous déplacer de la case départ D vers la case arrivée A.
On doit se déplacer seulement de gauche à droite et de haut en bas. Les deux cases hachurées sont interdites.
Il faut les contourner. La chenille va parcourir en les dénombrant tous les chemins possibles.

CLIQUER

Dénombrement des chemins

Pour arriver sur une case, nous sommes obligés de passer par celle qui est juste au-dessus : H ou bien par celle qui est juste à sa gauche : G.
Aussi le nombre de déplacements s'obtiendra-t-il tout simplement en ajoutant ceux de la case H à ceux de la case G.
Si la case G est bloquée alors le nombre de déplacements sera celui de H ; si c'est H qui est bloqué alors le résultat sera le même que pour G.
Ci-dessous, le nombre de déplacements possibles en partant de la case départ D s'inscrit dans chaque case.

CLIQUER

Ci-dessous, on cherche et on énumère tous les chemins partant de la première case de la grille vers la dernière.
Il suffit d'entrer le nombre de lignes et de colonnes de la grille.
Pour des raisons de place évidentes, ces nombres seront inférieurs ou égaux à 7.
Pour bloquer une case, il suffit de cocher le bouton correspondant.

Au démarrage de l'animation, une case au hasard est bloquée.
On peut bien entendu la débloquer ensuite.



CLIQUER

Analysons plus précisément la case notée C sur la figure ci-dessous.

En partant de D et en allant uniquement de gauche à droite et de haut en bas, tous les chemins ont une longueur de 7 pas (le pas étant la largeur d'une case). Pour chaque chemin, nous devons avancer de 5 pas vers la droite et 2 pas vers le bas. Notons d un pas vers la droite et b un pas vers le bas. Voici un exemple de codage de chemin : ddddbdb cela signifie 4 pas à droite, 1 pas vers le bas, 1 pas à droite et enfin 1 pas en bas. Le nombre de chemins différents correspond au nombre de possiblités de placer 5 d et 2 b dans la chaîne de 7 lettres formée uniquement de d et de b (21 possibilités pour C).

C'est donc tout à la fois le nombre de façons de positionner 5 d dans 7 places ou bien de placer 2 b dans ces 7 places.
On parle du nombre de combinaisons de 5 parmi 7 noté ou du nombre de combinaisons de 2 parmi 7 noté .
Nous avons: = = 21.
Pour arriver en C, nous sommes obligés de passer par la case juste au-dessus (chemin de longueur 6 avec 5 pas à droite et 1 vers le bas) ou par celle juste à sa gauche (longueur 6 avec 4 pas à droite et 2 vers le bas).
Nous avons donc .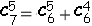

De façon générale si le chemin a une longueur n avec p pas à droite et (n-p) vers le bas. Le nombre de possibilités est 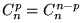. Pour la case juste au-dessus, la longueur est de (n-1) cases avec p pas à droite donc chemins différents et pour la case juste à gauche la longueur est de (n-1) avec (p-1) pas à droite donc 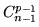possibilités.. Pour une case donnée, il faut paser soit juste au-dessus soit juste à sa gauche. Ainsi nous obtenons : .

Habituellement on raisonne ainsi : est le nombre de façons de positionner 2 b dans un mot de 7 cases. On a 7 possibilités pour le premier b puis 6 pour le deuxième. cela donne 6x7=42 cas.
Cependant les 2 lettres étant permutables de 2 façons, inous aurons =(6x7)/2.

De façon générale

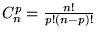
Le triangle de Pascal

Maintenant déplaçons-nous dans un triangle en suivant impérativement les directions : ou .

Notons sur chaque point, le nombre de chemins arrivant dessus. Pour arriver sur une case, nous devons passer obligatoirement par l'une des 2 cases juste au-dessus. Aussi, le numéro d'une case s'obtient-il en ajoutant ceux des 2 cases juste au-dessus. Nous obtenons le triangle de Pascal représenté ci-contre.

Très pratique pour calculer les puissances de polynômes...

la 6ème ligne donne les coefficients de (a+b)⁵ :

(a+b)5 = 1 a5 + 5 a4b + 10 a3b2 + 10 a2b3 + 5 ab4 + 1 b5

Les coefficients de (a+b)ⁿ sont donnés par la (n+1)^ième ligne et la somme des nombres de chaque ligne est une puissance de 2.
Les nombres de la (n+1)ème ligne ont une somme de 2ⁿ.
En effet, la (n+1)ème ligne donne par exemple les nombres de chemins de longueur n en fixant le nombre de pas descendant soit vers la droite ou vers la gauche.
Or pour chaque pas d'un chemin de longueur fixée on a deux possibilités : descendre à gauche ou bien à droite.
Pour n pas, nous aurons 2ⁿ possibiltés correspondant à la somme de toutes les combinaisons possibles pour obtenir un chemin de longueur n.

Les abeilles

Appelons A, B, C, D, E... les cellules dans les rayons de miel d'une ruche. La reine des abeilles fait sa ronde sur deux rangées de cellules, en partant de A. Elle se déplace uniquement de gauche à droite soit horizontalement soit obliquement.

	Elle a 1 seule possibilité pour arriver en B : AB. 2 chemins sont possibles pour arriver en C : AC et ABC Pour arriver en D, elle doit passer soit en C, soit en B, elle a donc ( 2 + 1) = 3 possibilités : ABD, ACD, ABCD.
Pour arriver en E, elle doit passer soit en C, soit en D, elle a donc (2 + 3 )= 5 possibilités : ACE, ABCE, ABDE, ACDE, ABCDE. De même on trouverait 8 possibilités pour arriver dans la cellule F celles de D plus celles de E. 1, 2, 3, 5, 8,... dans cette suite, chaque terme est la somme des deux précédents. Nous retrouvons la suite de Fibonacci, très naturel non ? ;o) (Cf les alvéoles hexagonaux des abeilles, mais aussi Fibonacci et le nombre d'or dans la nature)

Les rectangles et le pavage

Plaçons des rectangles de 2 sur 1 dans un rectangle de longueur n et de largeur 2.
De combien de façons pourra-t-on les disposer ?

Dans un rectangle de 2 sur 2, nous avons 2 possibilités :
ou

Dans un rectangle de 3 sur 2, nous avons 3 possibilités :
ou ou

Dans un rectangle de 4 sur 2, nous avons 5 possibilités :
ou ou ou ou

On trouverait 8 possibilités dans un rectangle de 5 sur 2.
2, 3, 5, 8... nous remarquons que chaque terme est la somme des 2 précédents.
Est-ce toujours vrai ? Dans ce cas nous aurions la suite de Fibonacci...
Appelons Pn le nombre de possibilités dans un rectangle de n sur 2, Pn-1 dans un rectangle de (n-1) sur 2, Pn-2 dans un rectangle de (n-2) sur 2, nous allons voir que nous sommes bien en présence de la suite de Fibonacci.

De deux choses l'une :
-soit la case n contient une pièce debout ;
  alors la case (n-1) contiendra ou une pièce debout ou une pièce couchée, peu importe.
  Dans ce cas nous avons toutes les Pn-1 possibilités venant du rectangle (n-1) sur 2.
-soit la case n contient une pièce couchée ;
  alors la case (n-1) contient forcément l'autre morceau de cette pièce couchée.
  Par contre la casqe (n-2) contiendra ou une couchée ou une debout peu importe.
  Nous avons les Pn-2 possibilités du rectangle (n-2) sur 2.

Finalement
Pn = Pn-1 + Pn-2
Nous obtenons bien la suite de Fibonacci qui commence par 1, 2, 3... etc. où chaque terme est la somme des deux précédents.

Suite de Fibonacci ! Sempiternelle suite de Fibonacci !

Pourtant son nom est frauduleux ! Leonardo Fibonacci (fils de Bonaccio) s'appelait Leonardo Pisano Bigollo, Pisano signifiant qu'il vivait à Pise, on ne sait quel est le sens de Bigollo... Etant le seul mathématicien de talent de son époque, l'importance de Fibonacci est parfois surestimée, cependant ses travaux sont fondamentaux comme lien entre les mathématiques arabes et celles de la Renaissance. Son influence est certaine dans l'introduction des nombres arabes en Occident.
Ne croyez pas non plus que la suite de Fibonacci est la clé de l'univers ! Méfiez-vous, il y a des faux ! Certaines suites lui ressemblent au début mais ce ne sont que simples coïncidences (Cf L'univers des nombres de Ian Stewart).