L'hyperbole
Le
problème
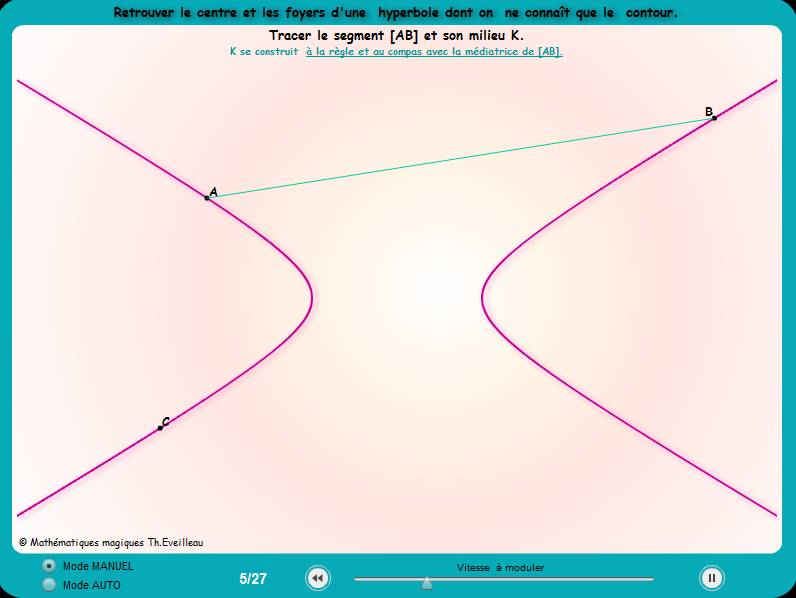
On
ne connaît que le contour de l'hyperbole : juste son tracé.
Retrouver ses éléments caractéristiques : foyer
et sommets rigoureusement construits à la règle et au
compas seulement.

SOLUTION
avec une construction animée pas à pas ou en mode automatique
Les commentaires soulignés en haut de l'animation sont des liens
renvoyant aux constructions de base à la règle et au compas
:
-médiatrice
d'un segment,
milieu d'un segment à la règle et au compas, à
partir de la médiatrice récédente,
parallèle à une droite passant par un point, bissectrice
d'un angle etc.
OU milieu au compas exclusivement.
D'autres animations
sur les coniques sont aussi disponibles.
L'animation peut être visualisée
- en mode pas à pas : on contrôle
en cliquant soit le bouton arrêt, avance ou recule ;
- en mode automatique (uniquement
jusqu'à l'étape 18) : l'animation se déroule
de façon automatique à la vitesse que l'on choisira.
On peut stopper, avancer manuellement puis reprendre le mode automatique.
A la dernière étape, le point H
tourne sur le cercle principal de
l'hyperbole.
On peut le déplacer manuellement en cliquant le bouton STOP
en haut à droite de l'animation.
On relance le mouvement automatique du point en cliquant le bouton ANIMER.
CLIQUER
La construction fait appel à une jolie
propriété : l'hexagramme
de Pascal dit hexagramme mystique.
Si on prend trois points P, Q, R alignés, puis trois autres
points alignés, p, q et r
alors
les intersections des droites (Pr) et (Qp)
puis de (Pr) et (Rp) et enfin
de (Qr) et (Rq) sont alignées.
De même
si on prend six points P, Q, R ,p, q et r sur une conique alors
les intersections des droites (Pr) et (Qp)
puis de (Pr) et (Rp) et enfin
de (Qr) et (Rq) sont alignées.
SOIT :
Les trois paires
de côtés opposés d'un hexagone inscrit dans
une conique se croisent en trois points alignés.
Ainsi en faisant se confondre deux des six points sur une conique,
nous pouvons construire à la "règle
seulement" la tangente en un point d'une conique.
C'est ce qui a été fait dans l'animation en choisissant
sur une branche de l'hyperbole quatre points arbitraires pour construire
uniquement avec des intersections de droites, la tangente en le
point M.
Cette tangente nous a permis de déterminer le foyer grâce
à la propriété illustrée dynamiquement
à la dernière étape de l'animation.
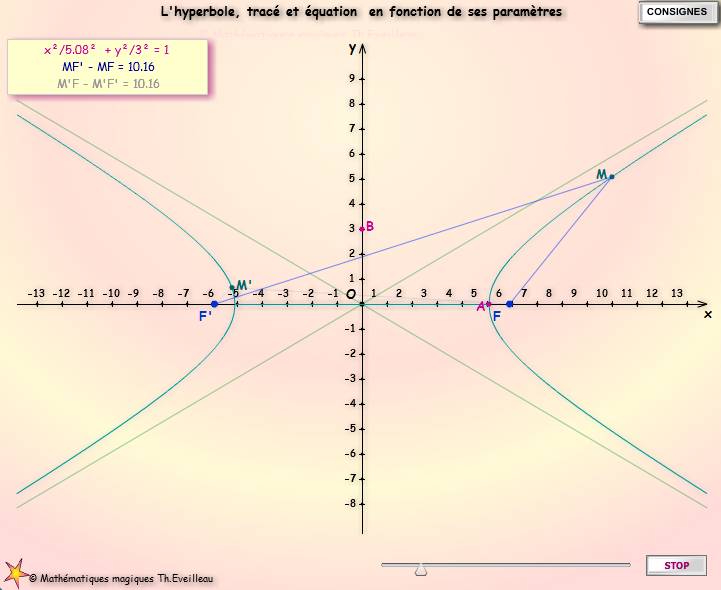
L'hyperbole,
équation rapportée à ses axes et quelques propriétés
L'équation
réduite de l'hyperbole dans le repère rapporté
à ses axes est :
x²/a² - y²/b² = 1
Les boutons STOP et ANIMER arrêtent
ou relancent le déplacement des points M
et M '.
On
peut déplacer MANUELLEMENT les points M
(SOURIS),
A
et B
(SOURIS ou
CLAVIER) après avoir
cliqué le bouton STOP.
Avec la SOURIS
Déplacer les points A
et B
pour modifier les paramètres de l'hyperbole.
Déplacer les points M et
M' avec la
SOURIS et
noter que |MF' -MF|
=2 a, est constant pour chaque hyperbole : |MF'
- MF| = 2 * OA.
Au CLAVIER
-les flèches HAUT et BAS
modifient le point B
;
-les flèches GAUCHE et DROITE
modifient le point A.
CLIQUER