En
hommage à Monsieur Johnson, Pierre Jullien a réalisé
l'image d'un 4-cube (cube à quatre dimensions) avec quatre cercles de
même rayon ayant un point commun.
Cette construction fait suite à la page 3
cercles pour un cube.
ANIMATION
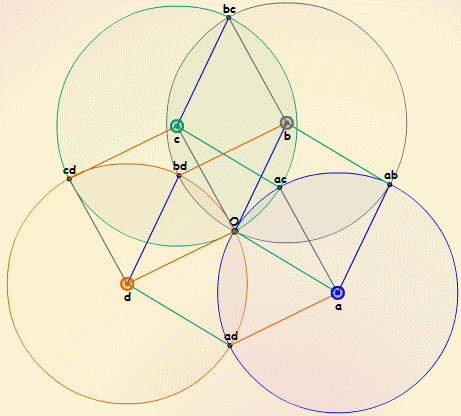
Les quatre cercles
de centres respectifs a, b, c et d, sont de
même rayon R. Ils ont tous les qutre un point commun O.
Traçons les quatre cercles passant par les points ab, ac, ad,
bc, bd, cd (autres que O) d'intersection de ces quatre cercles pris
trois par trois.
Nous introduisons
quatre nouveaux points que nous baptisons abc, abd, acd, bcd
qui sont les centres respectifs des cercles circonscrits aux triangles
de sommets ab, ac, bc puis ab, ad, bd puis ac, ad,
cd et enfin bc, bd, cd.
Nous traçons également le point E commun
à ces quatre derniers cercles.
Ci-dessous
on peut déplacer à tout instant les points a, b, c ou
d à la SOURIS ou bien au CLAVIER avec les quatre flèches.
Il est possible d'animer un seul, deux trois ou quatre points à
la fois.
Pour
plus de visibilité,
cacher ou non les cercles ou les côtés tracés
en cochant ou non le bouton adéquat.
CLIQUER
Les
cercles finaux de centres abc, abd, acd et bcd sont images des quatre
cercles de centres a, b, c et d dans un demi-tour du plan (1).
On peut voir huit
et même seize cercles tous de même rayon car chaque point
du 4-cube est centre d'un cercle passant par ses quatre voisins.


Les
segments [ab cd], [ac bd] et [ad bc] ont même milieu : le symétrique
de O par rapport au barycentre des quatre centres a, b, c, d.
C'est le centre C du 4-cube à venir.
Nous avons :

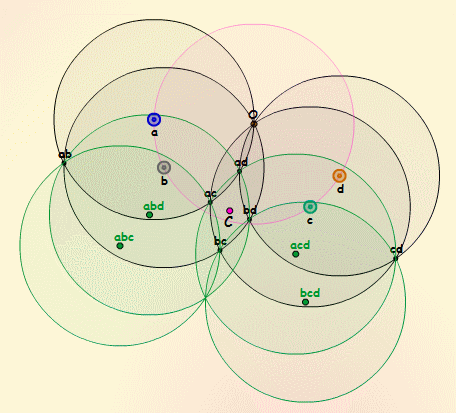
Les quatre cercles
verts ci-dessous de centres abc, abd, acd et bcd sont les symétriques
des quatre cercles initiaux de centres a, b, c et d, tracés en
gris ici, par rapport à ce point C.
Les
plus courageux pourront,
avec cinq cercles de même rayon ayant un point commun,
mettre en évidence l'image d'un 5-cube.

Avec
n cercles... nous aurions un n-cube.
Le problème des cercles a fait l'objet de
la deuxième composition du CAPES interne de 1999.
