PROBLEME
Un triangle quelconque... révèle une symétrie inattendue !
On parle souvent de la merveille de Morley.
Frank Morley (1860 - 1937) découvre en 1899 un théorème remarquable qui a échappé aux milliers de mathématiciens qui depuis Euclide ont exploré la géométrie plane.

Le théorème de Morley
Les points d'intersection des paires de trisectrices adjacentes des angles d'un triangle sont les sommets d'un triangle équilatéral.

"Given a triangle A, B, C the pairwise intersections α, β,γ of the trisectors form the vertices of an equilateral triangle"

Ce théorème a été apparemment ignoré en raison des incertitudes liées à la construction de la trisection.

VISUALISATION avec une ANIMATION


Déplacer à volonté les sommets A, B et C... et
observer le triangle équilatéral formé avec les points d'intersection des trisectrices.

CLIQUER





--------------------------------------------------------------------------------------

 

Si l'orientation est différente, alors les trisectrices extérieures interviennent dans ma figure.
Le triangle jaune reste équilatéral mais n'est plus intérieur au triangle ABC.

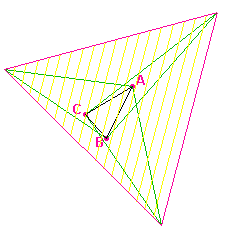
La démonstration "Ah Ah ! " de Conway L'idée géniale de Conway a été de construire un puzzle constitué de septtriangles qui vont permettre très simplement de reconstituer le triangle de départ. On part du triangle central équilatéral et on l'entoure de triangles dont les côtés et les angles sont définis de façon précise et astucieuse. Notons que la somme des angles d'un triangle est égale à 180° et donc que a+b+c =180°/3 = 60°. Un triangle équilatéral a trois angles égaux à 60°. On reconstitue naturellement le triangle original ABC comme indiqué ci-contre.

La démonstration de A.Letac

Depuis sa découverte ce théorème a suscité une véritable fascination et l'on a une quantité impressionnante de démonstrations.
Alain Connes (lauréat de la médaille Fields en 1982) en donne en 1998 une nouvelle et remarquable démonstration utilisant la théorie des groupes.

La démonstration proposée ci-dessous est celle de A.Letac 1939 (proposée dans le Sphinx n°9, problème n° 490).
Elle repose sur des calculs trigonométriques.

Dans le triangle ABC, notons 3a, 3b et 3c les mesures respectives des angles en A, B et C.
Nous avons donc a+b+c = π/3 et noterons σ = π/3.

Soit R le rayon du cercle circonscrit au triangle ABC. D'après la loi des sinus appliquée au triangle ABC nous avons . Dans le triangle BPC, cette loi des sinus donne donc et .

Avec la formule *

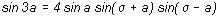
nous obtenons :
(1)
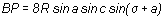
puis de la même façon,
(2)

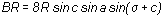
et le théorème d'Al-Kashi appliqué dans le triangle BPR donne

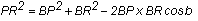
soit avec les résultats (1) et (2) précédents :
PR² = 64 sin² a sin² c (sin² (σ + a) + sin² (σ + c) - 2 sin(σ + a) sin(σ + c) cos b).
Puisque (σ + a) + (σ + c) + b = π, nous pouvons réutiliser le théorème d'Al-Kashi à un triangle
dont les angles seraient (σ + a) et (σ + c) et b et
dont les côtés seraient sin (σ + a), sin (σ + c) et sin b (en prenant le rayon du cercle circonscrit égal à 1/2).
Cela donne
sin² b =sin² (σ + a) sin² (σ + c) - 2 sin(σ + a) sin(σ + c) cos b.
Finalement, nous trouvons
PR = 8 R sin a sin b sin c.
Nous trouverions de même :
RQ = 8 R sin a sin b sin c
et
QP = 8 R sin a sin b sin c.
Conclusion : PR = RQ = QP.

Et le triangle PQR est bien équilatéral.

 

---

   

 

*
En effet
sin 3a = 3 sin a - 4 sin³ a
et

4 sin a sin (σ+a) sin(σ-a)  = 4 sin a (sin σcos a + sin a cos σ ) (sin σ cos a - sin a cos σ)
                                      = 4 sin a (sin² σcos² a - sin² a cos² σ )
                                      = 4 sin a (3/4 cos² a - 1/4 sin² a)
                                      = sin a (3 cos² a - sin² a)
                                      = 3 sin a (1 - sin²a) - sin³ a
                                      = 3 sin a - 3 sin³ a - sin³ a
                                      = 3 sin a - 4 sin³ a
Finalement on a bien :
4 sin a sin (σ+a) sin(σ-a) = 3 sin a - 4 sin³ a
puis