EXEMPLES
Près
de l'Euphrate, sur le site de Nippour, proche de l'ancienne Babylone
on a trouvé un grand nombre de temples datant d'environ 3000
ans avant notre ère. On y a découvert de nombreuses
statuettes, sculptures et tablettes témoins de l'activité
économique de l'époque. Sur des tablettes d'environ
1000 ans avant notre ère, on a observé une curieuse
procédure pour effectuer des multiplications.
Cette technique de multiplication des entiers nécessitait
uniquement de savoir faire des additions et peut-être des
soustractions.
Le scribe calculateur devait aussi disposer d'une table de carrés.
La multiplication se ramenait à une addition de carrés.
Pas très rapide ni très pratique... ce procédé
repose sur le fait que tout nombre entier peut se décomposer
en somme de carrés.
Table des carrés des entiers de 1 à 20.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
1
|
4
|
9
|
16
|
25
|
36
|
49
|
64
|
81
|
100
|
121
|
144
|
169
|
256
|
225
|
256
|
289
|
324
|
361
|
400
|
Deux exemples de multiplication utilisant cette technique babylonienne

soit
20² + 5² + 5² + 5² + 5²
|

soit
28² + 8² + 8² + 8² + 4² + 4²
|
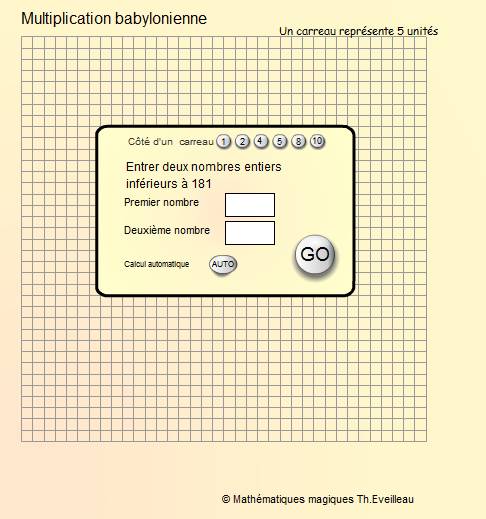
ANIMATION
Dans l'animation suivante,
essayer différentes valeurs après avoir choisi le
nombre d'unités représentées par le côté
d'un carreau de la grille dessinée.
Voici quelques exemples : (78,195) (36,15) (286,180) etc.
CLIQUER
Il
est très intéressant de relier
l'algorithme d'Euclide à ce petit problème
Quelle est la taille du plus grand carré qui pave exactement un
rectangle de dimensions données ?