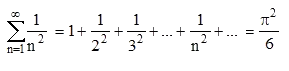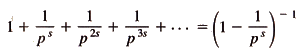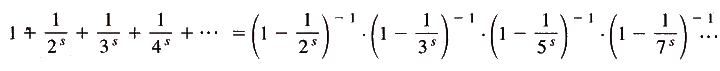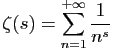Nombres
premiers entre eux et probabilité
LE PROBLÈME
Choisissons au hasard deux nombres entiers. Peu importe l'ordre de
grandeur.
Y-a-t'il plus de chance qu'ils
soient premiers entre eux ou qu'ils ne le soient pas ?
Ce problème d'arithmétique sur les nombres premiers
entre eux, va nous emmener en voyage vers les nombres premiers, les
probabilités, l'algèbre,
la fonction zéta bien connue des mathématiciens. Au
passage nous rencontrerons le nombre Pi.
ANIMATION
- CHOISIR le maximum des nombres entiers. S'il est
très grand le calcul sera un petit peu plus long même
en mode Ultra-Rapide.
- CHOISIR entre :
JOUER mode pas à pas pour une observation
de chaque étape ou
SIMULATION avec de multiples expériences consécutives.
-> CHOISIR le nombre d'expériences.
En mode JOUER, cliquer sur le bouton fléché
pour réaliser une nouvelle expérience ;
En mode SIMULATION, cliquer sur le bouton GO pour
lancer les expérimentations ;
- SI le bouton Ultra rapide est coché, le
résultat est immédiat.
- SINON chaque couple d'entiers tirés au sort est représenté
par le point (p,q) sur le graphique.
- si le couple est ROUGE
les entiers ont au moins un diviseur commun et ne sont PAS
premiers entre eux,
- si le couple est VERT
les deux entiers sont PREMIERS entre
eux.
Le pourcentage de couples d'entiers premiers entre
eux est affiché au cours de tous les tirages.
-Le bouton RAZ permet de tout réinitialiser.
-La VITESSE d'exécution est réglable
en mode SIMULATION .

SOLUTION
Il y a plus de chance qu'ils soient
premiers entre eux qu'ils ne le soient pas !
La réponse est environ 60.79271 % de chances d'obtenir des
nombres premiers entre eux.
La probabilité est rigoureusement : 6/π².
Étonnamment on retrouve le nombre transcendant π
!
Euler
(1707-1783), pour trouver ce résultat a mêlé différents
domaines mathématiques comme la théorie des nombres,
la trigonométrie, l'algèbre, les probabilités..
Nous allons donner ici les éléments essentiels de du
cheminement menant à ce résultat
Rappel : deux nombres entiers sont premiers entre eux s'ils n'ont
aucun autre diviseur commun que l'unité.
On peut aussi affirmer que leur Plus
Grand Diviseur Commun
est 1, VOIR ICI.
Voir aussi la décomposition d'un
entier en produit unique de facteurs premiers ICI.
Et la factorisation
géométrique ICI.
Nous savons par le théorème
fondamental de l'arithmétique que :
Tout entier se décompose de
façon unique en un produit de puissances de nombres premiers.
Pour
que deux nombres entiers soient premiers entre eux, il faut et il
suffit qu'ils n'aient aucun facteur commun dans leur décomposition
en facteurs premiers.
Analysons les facteurs p premiers possibles
dans les deux nombres entiers.
Soient a et b
les facteurs comparés, regardons petit à petit la probabilité
qu'ils ne soient pas tous les deux multiples d'un nombre premeir
p.
Avec les entiers pairs, p= 2, nous avons
un seul des cas :
- a pair, b pair
;
- a pair, b impair
;
- a impair, b
pair ;
- a impair, b
impair.
Ces quatre cas sont équiprobables.
La seule possibilité que les deux facteurs a
et b soient pairs est donc 1/4 = 1/2²
DONC pour que ces deux facteurs
a et b
ne soient pas tous deux pairs la probabilité
est 1 -1/2² = 3/2²
Avec p = 3, nous avons un seul des neuf
cas :
- a multiple de 3, b
multiple de 3 ;
- a a pour reste 1 dans la division par
3 , b a pour reste 0 dans la division par
3 ; (OU p congru à 1 modulo 3, q multiple de 3).
- a a pour reste 2 dans la division par
3 , b a pour reste 0 dans la division par
3 ;
- a a pour reste 0 dans la division par
3 , b a pour reste 1 dans la division par
3 ;
- a a pour reste 1 dans la division par
3 , b a pour reste 1 dans la division par
3 ;
- a a pour reste 2 dans la division par
3 , b a pour reste 1 dans la division par
3 ;
- a a pour reste 0 dans la division par
3 , b a pour reste 2 dans la division par
3 ;
- a a pour reste 1 dans la division par
3 , b a pour reste 2 dans la division par
3 ;
- a a pour reste 2 dans la division par
3 , b a pour reste 2 dans la division par
3.
Ces neuf cas sont équiprobables.
La seule possibilité que les deux facteurs a
et b soient multiples de 3 est donc 1/9
= 1/3²
DONC pour que ces deux facteurs
a et b ne soient pas tous deux multiples de 3 la
probabilité est 1 -1/3² = 8/3²
En prenant un entier premier p, nous poursuivons
le même raisonnement.
Nous obtenons p²
cas équiprobables.
La seule possibilité que les deux facteurs a
et b soient multiples de pest
donc 1/p²
DONC pour que ces deux facteurs
a et b ne soient pas tous deux multiples de p la probabilité
est
1
- 1/p²
Ensuite, nous avons p=5,
puis p=7, puis
p=11, etc.
Les probabilités pour différentes valeurs de p
premier sont indépendantes et donc on peut multiplier les probabilités
pour obtenir tous les facteurs entiers premiers possibles.
AINSI la probabilité
P que deux enteirs soient premiers entre eux (ils
n'ont aucun facteur commun premier) est :
P =
(1 - 1/2²) * (1 - 1/3²) * (1 - 1/5²) *
(1 - 1/7²) *...
(1 - 1/p²) * ...
Les points de suspension indiquant que le processus se poursuit sur
l'infinité des nombres p premiers.
Prenons l'inverse de P, nous avons
:
1/P =
1/(1 - 1/2²) *
1/(1 - 1/3²) *
1/(1 - 1/5²) *
1/(1 - 1/7²) *...
1/(1 - 1/p²) *
...
Cela s'écrit : 1/P
=  où le produit infini est étendu à
l'ensemble des nombres premiers.
où le produit infini est étendu à
l'ensemble des nombres premiers.
Euler a montré que cette dernière expression est précisément
la somme nommée  : Cf
remarques et démonstration
: Cf
remarques et démonstration
 avec
avec 
1/P
=
 =
= 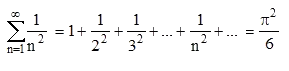
1/P
=  = π²/
6.
= π²/
6.
Ce problème est appelé le problème de Bâle
ou problème de Mengoli.
On peut en trouver diverses démonstrations sur le web et notamment
celle d'Euler qui a le mérite d'être assez accessible.
Son
inverse P
est donc
6/π².
La probabilité cherchée
est 6/π².


REMARQUES

 .est
un cas particulier de cette fonction suivante zéta de Riemann.
.est
un cas particulier de cette fonction suivante zéta de Riemann.

Avec l'exposant 2, cette série est convergente vers
π²/6.
DÉMONSTRATION
SOIT
s réel , s > 0 ;
p entier premier.
La somme de la série géométrique
de raison 1/ps est
: 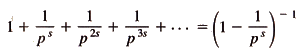
Multiplions membre à membre ces relations vérifiées
pour tout nombre premier p.
Nous obtenons tous les produits possibles de nombres premiers.
DONC en utilisant la décomposition des entiers en leurs facteurs
premiers, nous obtenons à gauche de cette équation
--> le produit des inverses de tous les nombres entiers.
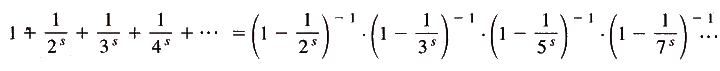
A gauche nous avons les puissances s des
inverses de tous les entiers et à droite le produit est appliqué
à tous les nombres premiers.
ET
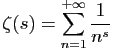
Cette formule
est due à Euler et elle sera exploitée plus tard par
Riemann (1826-1866) qui en déduira des résultats
sur la répartition des nombres premiers.
Finalement
 = 1/(1 - 1/2²) * 1/(1
- 1/3²) * 1/(1 - 1/5²)
* 1/(1 - 1/7²) *...
1/(1 - 1/p²) * ...
= 1/P =
π²/6
= 1/(1 - 1/2²) * 1/(1
- 1/3²) * 1/(1 - 1/5²)
* 1/(1 - 1/7²) *...
1/(1 - 1/p²) * ...
= 1/P =
π²/6
ENFIN P
=
6 /π²
==>
Retour

 où le produit infini est étendu à
l'ensemble des nombres premiers.
où le produit infini est étendu à
l'ensemble des nombres premiers. avec
avec