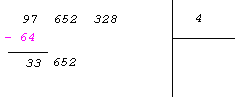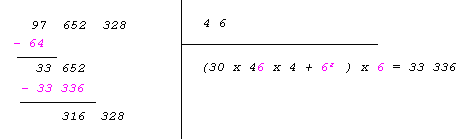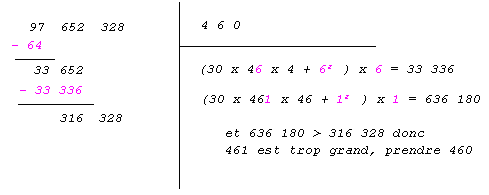|
Racine
carrée
à
la main
|
|
2
x 2 = 4
et 2 est la racine carrée de 4.
3 x 3 =
9
et 3 est la racine carrée de 9.
|
Les
calculatrices permettent de se soustraire à la difficulté
du calcul d'une racine carrée mais elles masquent en les décimalisant
la nature de ces nouveaux nombres.
Dans racine
carrée,
on entend racine,
qui évoque l'idée d'un nombre enfoui dans un autre,
et carrée,
qui renvoie pour ses deux significations, tant géométrique
qu'arithmétique, à la figure du carré, bien connue
depuis l'enfance.
Les racines carrées ont en effet leur origine dans le problème
consistant à trouver le côté d'un carré
dont l'aire est donnée
(dixit Stella
Baruk Dictionnaire de mathématiques élémentaires).
Menu
 Extraire
une racine carrée à la main : voir dynamiquement
Ci-dessous, entrer
un nombre entier plus petit que 100 000 000 et valider en cliquant
OK.
L'algorithme se déroulera petit à petit.
On peut le contrôler
avec les boutons interactifs :
arrêter, avancer ou reculer pas à pas avec les boutons
simples ;
déroulement automatique avec la double flèche avant.
La double flèche arrière repositionne au début.
Pour choisir un autre nombre cliquer le bouton RAZ.
CLIQUER
Description
de l'algorithme
 Ci-dessous,
un exemple extrait d'un manuel
de 1910 pour
le cours supérieur de certificat d'études - 11 à
13 ans.
Dans
cet exemple, on lit : " En 48 combien
de fois 6? Il y est 7 fois."
En réalité il y est 8 fois car
6 fois 8 font 48.
Cependant, 68x8=544, est trop grand pour 489.
Il faut donc comme pour les essais dans une division, prendre plus petit,
ici 7,
(dans les programes de l'époque
on n'étudiait que les entiers positifs pour le certificat d'études).
L'explication de cet extrait de 1910 peut paraître un petit peu
rapide.
En suivant pas à pas l'extraction de 1389 dans l'animation précédente,
on retrouve bien les mêmes étapes de calcul.
Voici maintenant ce même
procédé extrait d'un manuel
de Terminale
C et T de V.Lespinard
et R.Pernet 1968
REGLE
PRATIQUE
1.
Ecrire le nombre dont on veut extraire la racine comme le dividende
d'une division.
2.
Séparer en tranches de deux chiffres à partir de la
droite ; la dernière tranche à gauche peut n'avoir qu'un
chiffre.
3. Extraire
la racine de la première tranche à gauche ; on obtient
ainsi le premier chiffre de la racine cherchée qu'on écrit
à la place du diviseur habituel.
4. Retrancher le carré de ce nombre d'un chiffre de
la première tranche à gauche.
5.
Abaisser à droite du résultat de la soustraction précédente
(premier reste partiel), la tranche suivante.
6.
Séparer dans le nombre obtenu le dernier chiffre à
droite et diviser le nombre restant par le double du nombre d'un chiffre
écrit à la place du diviseur ; on écrit le double
de ce nombre à la place du quotient.
7. Si
le quotient est inférieur à 10 l'essayer, sinon commencer
par essayer 9 ; l'essai se fait en écrivant ce quotient à
droite du double de la racine de la première tranche et en
multipliant le nombre obtenu par le quotient considéré.
Si le produit peut être retranché du nombre formé
au 5, le quotient convient, sinon on essaie un nombre inférieur
jusqu'à ce que la soustraction soit possible.
8.
Le résultat de la soustraction est le deuxième reste
partiel. Ecrire le nombre essayé à droite du premier
chiffre écrit à la place du diviseur.
9.
Recommencer avec le deuxième reste partiel comme avec le
premier et ainsi de suite, jusqu'à ce que l'on ait utilisé
toutes les tranches. Le dernier reste partiel est le reste de la racine
carrée.
Un
exemple poussé après la virgule
.Il
faut partager le nombre décimal en tranches de deux chiffres
à partir de la virgule vers la gauche puis vers la droite,
en ajoutant des zéros à droite si c'est nécessaire.
.Ensuite
il faut extraire la racine carrée de l'entier obtenu en ne
tenant pas compte des virgules, mais placer une virgule à la
racine, quand on abaisse la première tranche décimale.
Mais
d'où vient le signe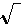 
?
.Le premier livre dans
lequel on mentionne ce signe serait de 1525.
Il s'agit de la 'chose' du mathématicien allemand Christian
Rudolff : nombre inconnu qu'il faut trouver.
Des manuscrits découverts d'abord à Dresde (1480), puis
à Vienne et à Göttingen montrent la transformation
d'un simple point (qui notait aussi la racine carrée en un
signe dans lequel un gros point fait à la plume est continué
par un trait d'abord un peu descendant puis montant.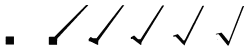 
Ce même type de signe 
est encore utilisé aujourdhui pour 'marquer' un texte que
l'on veut mettre en évidence. On sait que Rudolff a lu et
étudié ces manuscrits et a choisi une version stylisée
de cette marque sans barre supérieure. Le trait supérieur
est venu naturellement ensuite là où nous plaçons
aujourd'hui des parenthèses, par exemple pour chercher la
racine de (a + b).
Bibliographie
: A History of Mathematical Notation -Florian Cajori 1928
.Autre
explication de l'origine de ce signe : Amine m'a signalé
que le signe de la racine carrée est semblable au signe de
l'alphabet arabe qui désigne 'Jiim' équivalent
en Francais du 'J', et le nom de racine carrée en Arabe est
'jadr morabaa' ; 'jadr' ici veut dire racine. L'origine du
signe de la racine carrée serait arabe.
Recherche
arithmétique d'une racine carrée avec les 4 opérations
Cherchons
rapidement et très simplement la racine carrée de 5.
Elle est comprise entre 2 et 3.
Essayons le nombre 2,5 qui est juste au milieu de l'intervalle [2
3].
Alors 2,52=6,25 et 6,25>5 donc le nombre cherché
est compris entre 2 et 2,5.
Essayons 2,2. Alors 2,22=4,84 et 4,84<5 donc le nombre
cherché est compris entre 2,2 et 2,5.
Essayons 2,3. Alors 2,32=5,29 et 5,29>5 donc le nombre
cherché est compris entre 2,2 et 2,3.
Nous avons trouvé la première décimale : au
dixième près la racine de 5 est 2,2.
Continuons
avec 2,25.
Alors 2,252=5,0625 et 5,0625>5 donc le nombre cherché
est compris entre 2,2 et 2,25.
Essayons 2,22. Alors 2,222=4,9284 et 4,9284<5 donc le
nombre cherché est compris entre 2,22 et 2,25.
Essayons 2,24. Alors 2,242=5,0176 et 5,0176>5 donc le
nombre cherché est compris entre 2,22 et 2,24.
Essayons 2,23. Alors 2,232=4,9729 et 4,9729 <5 donc
le nombre cherché est compris entre 2,23 et 2,24.
Nous avons trouvé la deuxième décimale :
au centième
près la racine de 5 est 2,23.
Le procédé est simple
, en l'encadrant on se rapproche de plus en plus de la racine de
5.
Avec de la patience, on pourra ainsi approcher la racine de 5 d'aussi
près que l'on voudra, cependant nous ne l'atteindrons jamais
car la racine de 5 n'est pas un nombre décimal. De même
aucune fraction n'aura pour carré 5.
Alors on peut se demander si cette racine existe... Oui
elle existe et on la qualifie alors de nombre irrationnel
noté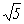 
Autres
méthodes
Il existe de nombreux algorithmes
pour calculer la racine carrée d'un nombre positif.
Ma
page sur le gnomon montre comment la trouver
à une unité près, avec de simples soustractions
de nombres impairs consécutifs.
Il
y a aussi une méthode géométrique
utilisant la règle et le compas.
Chez
les Babyloniens environ 5 siècles avant notre ère
:
une performance mathématique
impressionnante sur une tablette d'argile !
La longueur de la diagonale d'un carré a été
calculée ici avec une précision
de plusieurs chiffres après la virgule.
Le côté du carré : 30 donne
1/2 unité soit 30/60.
La diagonale du carré de côté
1/2 donne :
0 ; 42 ; 25 ; 35
i.e
42/60 + 25/60² + 35/603
soit environ 0,7071064815
Enfin ceci donne comme racine carrée de 2
:
1 ; 24 ; 51 ; 10
i.e 1
+ 24/60 + 51/60² + 10/603
soit environ 1,414212963
Cinq décimales (presque
six) sont exactes. |
 |
L'algorithme
de Héron d'Alexandrie
Chez les
mathématiciens grecs, extraire la racine carrée de
a revient à trouver un carré
dont l'aire est a :
on cherche un carré qui a la même aire qu'un rectangle
donné (origine agricole).
En prenant un rectangle de côté arbitraire x
et de même aire a, il est nécessaire
que l'autre côté ait pour longueur a/x.
Pour le rendre « moins rectangle », il suffit de considérer
un nouveau rectangle dont la longueur est la moyenne arithmétique
des deux côtés précédents soit
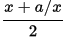et dont l'aire reste a.
En réitérant
infiniment le processus, le rectangle se transforme petit à
petit en un carré de même aire.
Pour déterminer la racine carrée du nombre (positif)
a, il convient dès lors de considérer la suite définie
par récurrence de la façon suivante :
.
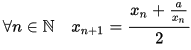Cet algorithme donne très vite un grand nombre de chiffres
significatifs.
Le calcul peut être commencé
avec n'importe quelle valeur différente de zéro.
.Exemple
avec la racine de 2 en partant de 1
x0= 1
x1 = ( 1 + 2/1) /2 = 3/2 = 1,5
x2= ( 1,5 + 2/1,5)/2 = 17/12 ~ 1,4166666
x3 = ( 17/12+ 2/(17/12))/2 = 577/408 ~ 1,41421568
x4 = ( 577/408+ 2/(577/408))/2 ~ 1,4142135
Nous avons déjà
5 décimales qui sont correctes : 1,41421
En
pratique on se fixe une précision et on arrête le calcul
lorsque la différence entre les deux derniers résultats
est inférieure à la précision souhaitée
soit 10-5 pour l'exemple ci-dessus.
On peut constater l'exceptionnelle efficacité de cet algorithme.
Dans
l'animation ci-dessous,
-choisir le nombre n dont on extrait la racine, puis l'approximation
intiale de cette racine ;
-cliquer les
flèches du bas pour voir les résultats.
Pour toute entrée de nombre au clavier,
il est INDISPENSABLE de valider en frappant la touche Entrée.
Sinon, utiliser les flèches des boutons adéquats.
On part d'un rectangle dont l'un des côtés a pour longueur
l'approximation entrée.
L'aire de chaque rectangle est toujours égale au nombre n
dont on extrait la racine.
Pour des raisons pratiques, l'échelle varie en fonction du
nombre n et de l'approximation initiale.
Mais bien entendu elle reste constante sur chaque exemple.
On voit petit à petit le rectangle
devenir de plus en plus 'régulier'
et tendre vers un carré.
CLIQUER
On affine pas à pas l'approximation
en cliquant la flèche en bas à droite de l'animation.
Le
mathématicien Héron d'Alexandrie
(Fin
1er siècle après J.C.)dans
ses Métriques,
explique cette méthode sur l'exemple de 720. Héron
favorisait les méthodes de calcul avec peu de démonstration
et beaucoup d'exemples.
"Comme 720
n'a pas son côté rationnel, nous pouvons obtenir son
côté avec une très petite différence
comme il suit. Le carré
immédiatement supérieur est 729 qui a 27 pour côté.
Divisons 720 par 27. Cela donne 
. Ajoutons 27 faisant 
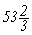dont nous prenons la moitié ou  .
Le côté de 720 est donc très approximativement
.
En effet si nous multiplions
par lui-même, le produit est  ,
si bien que la différence est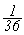 
. Si nous voulons avoir une différence plus petite que ,
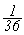nous prendrons
au lieu de 720, et en procédant de même nous trouverons
que la différence est beaucoup plis petite que ."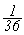
En fait dans l'algorithme,
Héron prend la seconde approximation puis la troisième
s'il y a lieu, le procédé pouvant être réitéré
à l'infini.
Source : mathématiques
et mathématiciens de Jean.Itard
Extraire
une racine cubique à la main
Le principe ressemble
à celui de l'extraction de la racine carrée.
Exemple
Extrayons la
racine cubique de 97 652 328
On découpe le nombre de
3 en 3 en partant de la droite 97
652 328.
Puis
on cherche le nombre dont le cube est le plus proche par défaut
de 97. C'est 4 dont le cube est
64.
On soustrait 64.
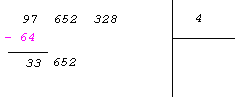
On
cherche alors le plus grand nombre a
tel
que
( 30 x 4a
x 4 + a2
)
x a
<= 33 652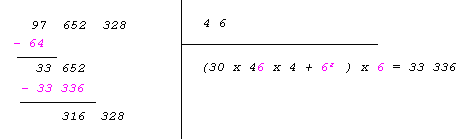 
Rq : 4a
est le nombre constitué de 4 dizaines
et de a unités.
On
cherche alors le plus grand nombre a
tel
que
( 30 x 46a
x 46 + a2
)
x a
<= 33 652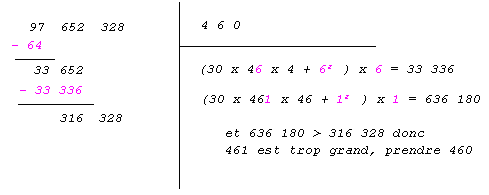 
Rq : 46a
est le nombre constitué de 46
dizaines et de a unités.
Finalement la
racine cubique de 97 652 328
est 460 à 1 unité près par défaut.
On
peut vérifier le résultat en l'élevant
à la puissance 3 ou
sur calculette en calculant 97
652 328 à la puissance (1/3) |
Autre
exemple extraction
au centième près de la racine cubique de 4568
Rq : De façon
générale, pour extraire la racine nième,
il suffit d'élever à la puissance (1/n) .
Et
les nombres négatifs...
Dans
l'ensemble des nombres réels on ne peut pas extraire la racine
d'un nombre négatif puisque le carré d'un nombre réel
est toujours positif ou nul.
Cependant le mathématicien italien Raffaele
Bombelli fut le
premier à évoquer et utiliser les racines ayant un carré
négatif en 1572 dans Algebra.
Ces nombres' impossibles' choquaient et furent appelés 'imaginaires'
par Descartes
un peu plus tard.
Ce n'est qu'avec Leonhard
Euler en 1777
que le sulfureux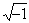 
devint le nombre connu aujourd'hui sous le nom de
i.
Puis Gauss
travailla sur les nombres complexes x+iy
représentés dans le plan par les points de coordonnées
x et y.
|
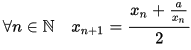Extraire
une racine carrée à la main : choisissez votre
nombre
