Tables
de multiplication fleuries
De
jolies images réalisées avec les tables de multiplication
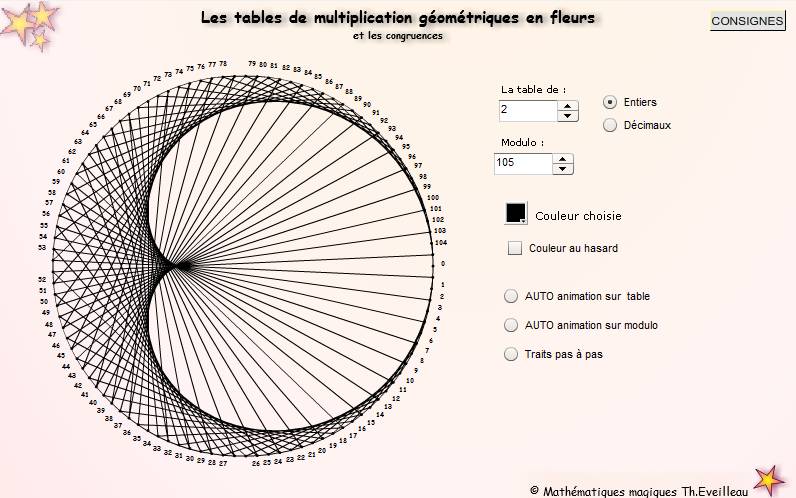
L'animation
suivante donne une représentation géométrique des
tables de multiplication en arithmétique modulaire.
- Entrer la table de multiplication : t .
Selon l'option choisie,
le nombre t
peut être un nombre entier
ou un nombre décimal pour une évolution
plus lente et plus
troublante.
- Ensuite entrer le modulo m : nombre par lequel on
divise les produits de la table t , pour obtenir
leur reste dans la division par ce modulo.
Le cercle est alors partagé équitablement en m
parties numérotées de 0
à m - 1.
Chaque produit t * i est relié au reste
dans la division par m pour i variant de 0
à m - 1.
- On peut faire varier la table de multiplication.
- On peut faire varier le modulo : c'est à dire le diviseur avec
lequel on obtient le reste qui sera relié.
On peut animer la construction de la table, produit par produit pour
chaque table fixée et pour chaque modulo fixé.
NE pas HESITER à modifier les valeurs de la table et du modulo
avant chaque animation.
Avec le curseur on peut moduler la vitesse des animations.
A
vos produits en dentelle !
CLIQUER
REMARQUE
Avec
la table de 2 nous obtenons une cardioïde que nous avons
déjà rencontrée ICI.
Lorsqu'un
rayon lumineux arrive sur le bord circulaire d'un récipient,
il est réfléchi symétriquement par rapport à
la perpendiculaire à la tangente
menée au point de contact de ce rayon sur le bord du récipient.
Les deux angles colorés en jaune ci-dessous sont égaux.
Cette symétrie correspond à la numérotation
n --> 2n des points tracés ci-dessus.
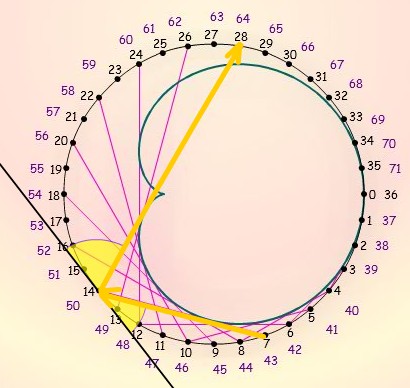
C'est pourquoi nous retrouvons cette cardioïde lumineuse lorsqu'un
récipient est correctement éclairé.

|