Le segment, le carré et l'infini...

"Le silence éternel de ces espaces infinis me terrifie" – Pascal

Juste avant les mathématiques "modernes", Cantor et Dedekind

C'est le 5 janvier 1874 que Cantor pose le problème qui va ébranler toutes les mathématiques avant qu'elles ne deviennent "modernes" :
"A propos des questions qui m'ont occupé ces derniers temps, je m'aperçois que, dans cet ordre d'idées, se présente aussi la suivante : est-ce qu'une surface (par exemple un carré, frontière comprise) peut être mis en relation univoque (en bijection) avec une courbe (par exemple un segment de droite extrémités comprises), de telle sorte qu'à tout point de la surface corresponde un point de la courbe, et réciproquement à tout point de la courbe un point de la surface ?".
Le 20 juin 1877, Cantor adresse à Dedekind une démonstration de ce résultat troublant : il existe une bijection entre le côté d'un carré et l'intérieur d'un carré, c'est-à-dire entre un objet de dimension 1 et un objet de dimension 2.
Le 25 juin, Georg Cantor lui envoie une nouvelle démonstration. N'ayant pas de réponse immédiate, il écrit alors le 29 juin ces phrases :
"Ce que je vous ai communiqué tout récemment est pour moi si inattendu, si nouveau, que je ne pourrai pour ainsi dire pas arriver à une certaine tranquillité d'esprit avant que je n'aie reçu, très honoré ami, votre jugement sur son exactitude. Tant que vous ne m'aurez pas approuvé, je ne puis que dire :
" Je le vois, mais je ne le crois pas ! "

Le 2 juillet 1877, Dedekind répond enfin :
" Cher ami, je suis entièrement convaincu par votre démonstration. "     

L'animation pour comprendre

Il s'agit d'illustrer étape par étape le résultat troublant établi par Cantor :
le segment et le carré ont autant de points l'un que l'autre.

- Pour passer à une étape suivante, cliquer la flèche droite en bas du cadre quand elle apparaît.
  Dans certaines étapes, des pauses de une ou plusieurs secondes sont normales et
  permettent la lecture de commentaires affichés en haut du cadre de l'animation.
- Il est possible, au cours de certaines étapes, de modifier la vitesse de déroulement avec le curseur fléché du bas de l'animation.

A la fin de l'animation, lors de l'étape 9, on peut faire correspondre dynamiquement les points du segment avec ceux de l'intérieur du carré.
Il suffit alors de déplacer avec la souris le point à l'intérieur du carré ou le point du segment.
Les coordonnées et les points sont automatiquement mises à jour.

Observer alors la composition des décimales de chaque point. Des couleurs facilitent la compréhension.

Cliquer




Le segment et le carré ont autant de points l'un que l'autre.

Animation permettant de voir d'emblée la bijection entre les points de l'intérieur du carré et ceux du segment

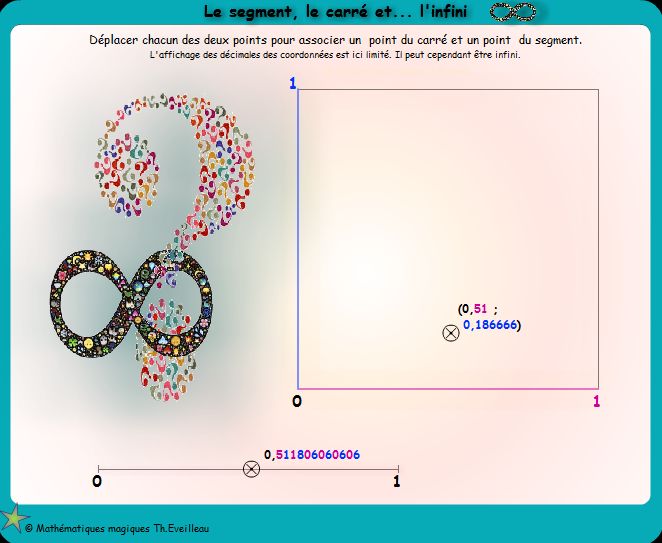
Déplacer chacun des deux points à l'intérieur du carré ou bien dans le segment.
Le point correspondant sera mis à jour de même que les coordonnées colorées de chacun des deux points.

 

Cliquer l'image

L’infini est depuis toujours dans la tête des hommes sans pour autant qu’ils arrivent à l’appréhender.
Dans ma page Zénon d’Élée, nous voyons que déjà dans l'antiquité, Zénon d’Élée présente une première approche de l'infiniment petit par le biais d’un paradoxe.

Georg Ferdinand Ludwig Philipp Cantor (3 mars 1845, Saint-Pétersbourg – 6 janvier 1918, Halle) est un mathématicien allemand, connu pour être le créateur de la théorie des ensembles. Il définit les ensembles infinis et les ensembles bien ordonnés.
Le travail de Cantor est d'un grand intérêt philosophique (ce dont il était parfaitement conscient) et a donné lieu à maintes interprétations et à maints débats.
Cantor a été confronté à la résistance de la part des mathématiciens de son époque.
Poincaré, bien qu'il connût et appréciât les travaux de Cantor, avait de profondes réserves sur son maniement de l'infini.
Les accès de dépressions récurrents du mathématicien, de 1884 à la fin de sa vie, ont été parfois attribués à l'attitude hostile de certains de ses contemporains.

Au XXIe siècle, la valeur des travaux de Cantor n'est pas discutée par la majorité des mathématiciens qui y voient un changement de paradigme, à l'exception d'une partie du courant constructiviste qui s'inscrit à la suite de Kronecker.
David Hilbert défenseur de Cantor a affirmé : « Nul ne doit nous exclure du Paradis que Cantor a créé. ».

 
Reproduction autorisée de Jean Pierre Petit, dans le Logotron, page 18