Le segment qui se voulait aussi grand qu'une droite...

Le petit segment a autant de points que tout segment plus long que lui.

Ci-dessous, déplacer avec la souris les points mobiles : N, B, M ou D.
 

Cliquer f

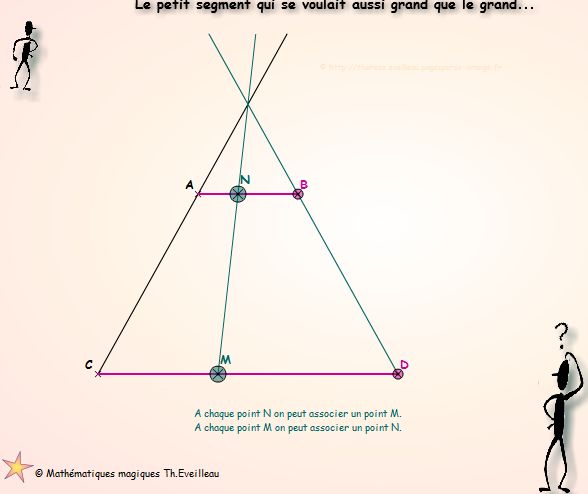
A  chaque point N de[AB],  correspond  un point unique M de [CD].
Et à chaque point M de [CD] correspond un point unique N de [AB]. 
Chaque point de chaque segment a son correspondant sur l'autre.

Cliquer l'image pour OUVRIR le swf

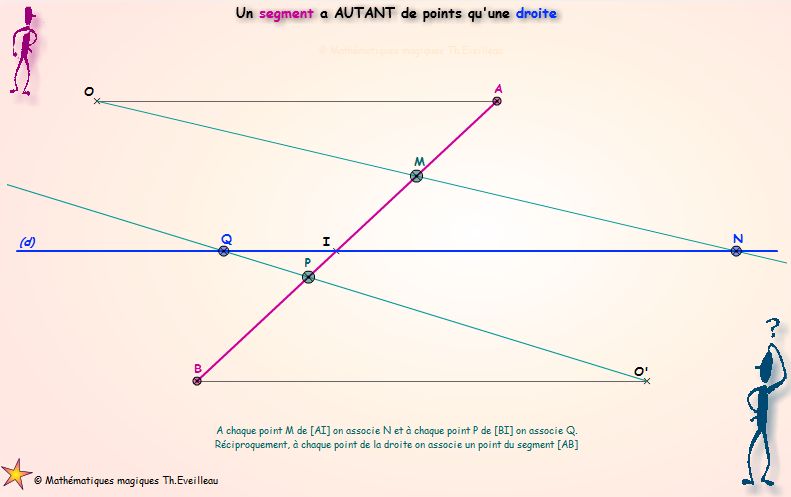
A chaque point M de la partie [AI] de [AB] correspond un point N de (d),
A chaque point P de la partie [BI] de [AB] correspond un point Q de (d).
A tout point du segment correspond un point de la droite et réciproquement.

Le segment et la droite ont autant de points l'un que l'autre.  

Le côté du carré a autant de points que le carré.
Voir la page avec animation ICI.

Nous utiliserons pour chaque nombre décimal l'écriture comprenant une infinité de zéros après la dernière décimale non nulle (par exemple 7/10 = 0.7000... ). Chaque réel de ]0,1[ a ainsi une écriture décimale unique.
Nous allons prendre comme unité la longueur du côté du carré.
]0,1[ représentera l'ensemble des points intérieurs au segment et ]0,1[ x ]0,1[ l'ensemble des points intérieurs au carré.
Montrons que le côté du carré a au moins autant de points que le carré :

A chaque point du segment correspond un point unique du carré
A chaque point x_s du segment, on fait correspondre un point unique (x_c,y_c) du carré de la façon suivante.
On écrit :
         x_s= 0,a₁a₂b₁b₂c₁c₂d₁d₂e₁e₂f₁f₂... avec a₁ chiffre des dixièmes, a₂ des centièmes, b₁ des millièmes etc...
_{et on pose :}
x_c = 0,a₁b₁c₁d₁e₁f₁g₁... et y_c = 0,a₂b₂c₂d₂e₂f₂g₂...
 
Le découplage des décimales de x_s donne l' abscisse et l'ordonnée d'un point unique (x_c,y_c) du carré.

Exemple
A partir du point d'abscisse 0,1263104579... du segment
            on obtient le point du carré
            d'abscisse 0,16147...
            et d'ordonnée 0,23059...

Remarque
cette fonction n'est pas injective car les deux points distincts du segment 0.019293949596... et 0.110203040506...
ont la même image (0.100... ; 0.123456...) (nous avons 0.1 = 0.099999... ).

A chaque point du carré correspond au moins un point du segment
(ce qui signifie que la fonction est surjective)

Au point (x_c,y_c) du carré avec
x_c = 0,a₁b₁c₁d₁e₁f₁g₁... et y_c = 0,a₂b₂c₂d₂e₂f₂g₂...
on associe
         x_s= 0,a₁a₂b₁b₂c₁c₂d₁d₂e₁e₂f₁f₂... obtenu en alternant les décimales de x_c et y_c.

Exemples
1/3 = 0,3333...
2/3 = 0,6666...
            Au point (1/3,2/3) du carré
            correspond le point 0,36363636... du segment
            soit exactement le point d'abscisse 36/99 du segment. 

Nous venons de démontrer que le segment a au moins autant de points que le carré !
et comme on peut le plonger dans le carré, il a autant de points que le carré.

Juste avant les mathématiques "modernes", Cantor et Dedekind

C'est le 5 janvier 1874 que Cantor pose le problème qui va ébranler toutes les mathématiques avant qu'elles ne deviennent "modernes" :
"A propos des questions qui m'ont occupé ces derniers temps, je m'aperçois que, dans cet ordre d'idées, se présente aussi la suivante : est-ce qu'une surface (par exemple un carré, frontière comprise) peut être mis en relation univoque (en bijection) avec une courbe (par exemple un segment de droite extrémités comprises), de telle sorte qu'à tout point de la surface corresponde un point de la courbe, et réciproquement à tout point de la courbe un point de la surface ?".
Le 20 juin 1877, Cantor adresse à Dedekind une démonstration de ce résultat troublant : il existe une bijection entre le côté d'un carré et l'intérieur d'un carré, c'est-à-dire entre un objet de dimension 1 et un objet de dimension 2.
Le 25 juin, Georg Cantor lui envoie une nouvelle démonstration. N'ayant pas de réponse immédiate, il écrit alors le 29 juin ces phrases :
"Ce que je vous ai communiqué tout récemment est pour moi si inattendu, si nouveau, que je ne pourrai pour ainsi dire pas arriver à une certaine tranquillité d'esprit avant que je n'aie reçu, très honoré ami, votre jugement sur son exactitude. Tant que vous ne m'aurez pas approuvé, je ne puis que dire :
" Je le vois, mais je ne le crois pas !"

Le 2 juillet 1877, Dedekind répond enfin :
"Cher ami, je suis entièrement convaincu par votre démonstration."     

 
Reproduction autorisée de Jean Pierre Petit, dans le Logotron, page 18


Dans le même ordre d'idées, il y a aussi autant de points dans l'espace que sur une simple droite !