Comment est né ce 3ème crible       1- Préambule       2- USA, côte Est      3- Number Theory       4- Un vice de plus      5- Un crible en deux heures chrono...

Démonter la "mécanique" de la multiplication       1-1 Quelques expériences visuelles       1-2 Conclusions sur les expériences précédentes      1-3 La réponse au pourquoi de la multiplication

Le troisième crible...
ou comment construire l'ensemble des nombres premiers à la règle et au compas

 

Le troisième crible : constructions et propriétés
(Emmanuel Rossignol - Astrium-GFI, avril 2002) 

1- Démonter la mécanique de la multiplication

     1-1 Quelques expériences visuelles :

     J'ai maintes fois expliqué de vive voix à plusieurs de mes amies (-e) mathématiciennes (-ne) le cheminement qui m'avait amené autrefois à " découvrir " le 3ème crible géométrique premier. Je ne puis exposer succinctement ici cette " aventure ", mais disons pour " faire court " que tout cela est né d'une simple interrogation : " Pourquoi l'Humain a-t-il inventé la multiplication ?… "
     Je préfère donc dans la suite de ce papier amener ma lectrice, ou mon lecteur ⁽¹⁾ , à découvrir et à " sentir ⁽²⁾ " par elle-même les points importants qui jalonnent la voie menant au dit crible.

     Commençons par nous concentrer sur la figure ci-dessous ⁽³⁾ :

 

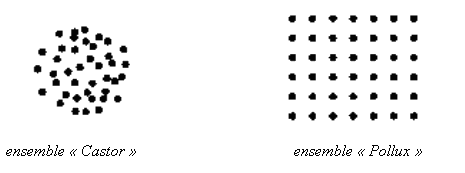
     Les ensembles " jumeaux " Castor et Pollux sont nés avec le même nombre d'éléments, ici les tâches noires que nous appèlerons par la suite " Points ". Ma lectrice (oml) aura peut être déjà pris soin d'évaluer le cardinal de ces jumeaux… Et comme je viens de lui donner une indication sur l'égalité liant les deux cardinaux… Mais cela n'est pas très grave en soi, nous allons recommencer tout de même. Il vous faut vous laisser porter par mes instructions.
     J'invite ma lectrice (oml) à prendre maintenant un crayon et à compter, ou re-compter, le nombre d'éléments de Castor ou Pollux - au choix - en moins de 3 secondes, une seule opération vous est accordée…
     Demandez le cas échéant à l'un de vos proches de vous chronométrer et tentez d'aller de plus en plus vite…
     …
     Bon ! je pense que vous avez le résultat, mais il n'est pas si important que cela en soi. Par contre plus de 95% d'entre vous ont évalué le cardinal de Pollux plutôt que celui de Castor. Même ceux et celles qui avaient précédé mes instructions. Une question à laquelle nous répondrons par la suite est celle-ci :
     Q - Pourquoi Pollux plutôt que Castor ?

     Trivial ! objectera la majorité. " C'est plus facile avec Pollux !… Une " bête " multiplication suffit, et on " voit " bien l'arrangement 6 par 7 !… ", ou " 7 par 6 ".
     Exact, on " voit " dans Pollux des " pré-découpages " en sous-ensembles égaux en termes de cardinal. Deux " choix " nous sont d'ailleurs offerts : " Pollux est constitué de 6 sous-ensembles de 7 points ", ou " Pollux est constitué de 7 sous-ensembles de 6 points ". Jusque là en termes opératoires c'est élémentaire : " on a compté 6 dans un sens, puis 7 dans l'autre et hop ! 6x7 = 42 "…

     Maintenant, j'affirme que plus de 80% des lectrices (odl) ont compté les bords de Pollux… Pas vous ! Ah… Si vous êtes enseignante() amusez vous à demander à une classe entière de " compter Pollux " et observez bien, c'est très précisément là qu'intervient le crayon : il faut observer attentivement où le " cobaye " le pose. Si a contrario vous n'êtes pas enseignante(), tentez l'expérience avec plusieurs de vos proches…

     Nous allons maintenant tenter à nouveau l'expérience, mais cette fois-ci avec nos deux ensembles jumeaux quelque peu " modifiés " ; Castor & Pollux ont tout deux " bougé " :

 

     Je pense que vous avez désormais réalisé que Castor et Pollux possédaient toujours le même nombre d'éléments, mais cette fois-ci - et tâchez de réfléchir à ce que vous avez observé il y a juste quelques secondes - votre attention n'a pas été particulièrement attirée par Castor, dont la " forme générale " et la " densité " des points vous ont semblés identiques à celle de la figure 1, par contre pour Pollux il y a fort à parier que quelque chose a " accroché " votre ligne de vision ⁽⁴⁾ … Allons, allons !… A celles (oc) qui contestent je demande de ne pas fixer un point de Pollux en particulier, mais plutôt d'essayer de regarder " globalement ⁽⁵⁾ " et de faire varier la distance entre vos yeux et la feuille.
     …
     Livrez vous maintenant au même exercice avec Pollux sur la figure 1.
     …
     Voilà ! pour clôturer là notre préambule expérimental il me reste à vous avouer que j'ai construit la figure 2 en faisant tourner Castor sur lui-même d'un angle nettement plus important que Pollux. D'autre part les points de Castor n'ont absolument pas bougé les uns par rapport aux autres, alors qu'un point⁽⁶⁾ de Pollux est source pour nous d'un " agacement " visuel.

     1-2 Conclusions sur les expériences précédentes :

     Nous pouvons affirmer d'après ce qui précède que le cerveau ⁽⁷⁾ humain est " sensible " à la " régularité ". Je mets volontairement entre guillemets les deux termes les plus critiques de la précédente phrase car je dois préciser plus avant ce que j'entends pour chacun des deux.
     Pour celles (ec) qui ne connaissent pas les outils de base employés par les spécialistes du Traitement de l'Image, nous pouvons dire que Pollux-1 nous paraît harmonieux. " Rien ne cloche " en quelque sorte, dans la disposition de ses points. Tout cela est " bien rangé ". On sent - ou voit ⁽⁸⁾ - qu'il y a une règle de construction, que les points sont " bien sages ". La disposition des points est telle que si Pollux était " immense " - disons 2 mètres par 2 mètres, donc 160 000 points environ - alors en parcourant des yeux le centre de ce Super-Pollux nous ne pourrions pas en distinguer un plutôt qu'un autre. Pour s'en convaincre il suffirait d'essayer de choisir un point au hasard au centre de Super-Pollux ⁽⁹⁾ , de fermer les yeux puis de secouer - gentiment, SVP - la tête, et enfin en ouvrant les yeux retrouver le point que l'on avait initialement choisi.
     Vous pouvez le faire !!… Bon rendez-vous à Toulouse ou des amis et moi-même serions vraiment heureux de vous connaître !… Une telle aptitude, çà s'étudie ! Par contre, imaginez maintenant que Super-Pollux possède un point " turbulant ⁽¹⁰⁾ ", très exactement comme Pollux dans la figure 2. Alors il est garanti que l'expérience imaginée au précédent paragraphe trouverait une issue heureuse à chaque fois, en choisissant précisément le point " pas comme les autres ". Une île en plein milieu de l'océan çà se remarque ! surtout quand on a ramé longtemps. Attention ! je ne dis pas que retrouver le point " agité " serait alors instantané, mais vous y parviendriez même - et surtout - en ne concentrant pas votre regard sur les points un par un ⁽¹¹⁾.
     Pour celles (ec) qui possèdent le bagage mathématique des Traiteurs de Signaux et d'Images - TSI par la suite - il est certain qu'elles (i) ont précédé mes pensées : la TF-bi d'un réseau de Diracs… etc. … A celles (ec) là je donne rendez-vous à l'annexe 1 pour une évocation plus rigoureuse des critères de régularité d'un réseau plan " humainement qualifiable pour la multiplication ". Une petite connaissance des œuvres de Victor Vasarelli est un plus…

     La première conclusion que nous pouvons tirer aussi bien des expériences menées lors des 2 premières pages que de celles imaginées plus haut nous permettent de supposer que " quelque chose " dans notre système visuel " de base " - que l'on peut réduire à un seul œil suivi de son nerf optique plus les premières (?) couches de neurones qui y sont connectés - est " construit " ou bien programmé - peut-être les deux ensemble ? - pour détecter les figures planes régulières, uniformes, comme Pollux-1 par exemple ou un ciel parfaitement bleu. L'indice qui nous permet d'affirmer cela est précisément le fait que lorsque on introduit une " petite " imperfection au beau milieu de ce qui est en apparence régulier, harmonieux, uni, alors les couches " inconscientes " de notre cerveau alertent celles qui " analysent " en quelque sorte, celles qui constituent la conscience. Autrement dit, nous n'avons pas besoin de penser consciemment pour dénombrer Pollux. Tout se passe mécaniquement tant que les nombres mis en jeu - ceux que l'on compte sur les 2 cotés de Pollux - sont inférieurs à 10, qui est la limite des tables de multiplication que nous avons tous apprises à l'école primaire.
     Pour bien " enfoncer le clou ", afin de définitivement convaincre les plus perplexes d'entre vous toutes (vt), je mentionnerai qu'il est une autre activité que nous pratiquons tous quotidiennement de façon " procédurale " sans que la " pensée active " viennent interférer dans l'acte. C'est la conduite automobile. Rappelez vous que vous êtes venues (-e) au Monde sans rien savoir ni comprendre du fonctionnement d'un dispositif d'embrayage et de ses interactions avec un moteur à explosion et une boîte de vitesses à pignons synchronisés ⁽¹²⁾ . Et pourtant ! vous pouvez néanmoins parcourir des dizaines de kilomètres en ville, et aux heures de pointe, sans vous préoccuper le moins du monde de l'ordre des actions - complexes - ni du timing précis avec lequel il faut l'exécuter. C'est simplement que vous avez toutes (-te) appris ces séquences d'actions qui sont devenues un élément de votre mémoire procédurale⁽¹³⁾ . 

     L'énumération de la suite des nombres - si l'on se cantonne aux " petits " nombres entiers - utilise les mêmes procédés mentaux. Et si vous réfléchissez encore une fois à la façon dont vous avez " compté " Pollux-1, alors vous devrez convenir que vous avez récité la " petite musique des nombres " - apprise dès l'école maternelle - et le métronome qui vous a servi n'était rien d'autre que le crayon parcourant les points l'un après l'autre avec d'ailleurs assez de régularité il faut en convenir. La " petite musique⁽¹⁴⁾ " s'est arrêtée net lorsque la ligne que vous suiviez alors du crayon ou du regard s'est terminée. La mise en mémoire du dernier nombre " chanté " s'est alors effectuée, et vous avez répété le même processus dans l'autre sens. Puis finalement pour trouver le résultat demandé, une " autre musique " - ou plutôt un fragment bien déterminé d'une " autre musique ", celle là aussi apprise dès l'enfance - vous est revenue à l'esprit et le résultat a jailli. " 6 fois 7, 42 ! ". 

     1-3 La réponse au " Pourquoi " de la multiplication : 

     Certaines (-e) d'entre vous doivent se dire que je " déraille " quelque peu à tenter de fournir un " Pourquoi " à la multiplication alors que jusqu'ici je me suis surtout concentré sur le " Comment " ; ou pour être vraiment exact, sur un des " Comment "[s]…
     " Comment ! me rétorquerez-vous, mais personne n'a attendu cet énergumène pour connaître " Le Comment " de la multpitplication !… ". Et vous avez (presque) raison. En effet, si l'on prend la définition la plus couramment admise de la multiplication on trouve dans la littérature mathématique des " fondements " :

     " La multiplication est définie comme l'addition, par récurrence… "  ⁽¹⁵⁾

     Et depuis les balbutiements des Mathématiques toutes les civilisations ayant développé des mathématiques ont tiré de cette définition " fonctionnelle " - le " Pourquoi " - diverses définitions " opératoires " - le " Comment ". Il est cependant important de pouvoir donner une définition " fonctionnelle " d'un objet mathématique faisant partie des fondements depuis l'origine car ce faisant, on peut dès lors rechercher si d'autres objets apparentés sont aptes à remplir la même " fonction ". On peut alors espérer résoudre, si l'on réussit à trouver des objets différents remplissant la même " fonction ", des problèmes ardus qui ne sont l'apanage que d'un seul d'entre eux. Par exemple l'avion, le train et le cheval, sont des moyens dont la fonction est de transporter l'humaine (-e) d'un point A de la planète à un autre point B. Malheureusement on sait aujourd'hui que les deux derniers moyens cités sont inopérants dès lors que je vous impose : A = Toulouse et B = New-York !…⁽¹⁶⁾ 

     Ainsi donc, vous devez regarder la suite de cette page comme une " vue " supplémentaire qui vous est offerte sur l'opération de multiplication. 

     Si l'on considère comme justes - fondées par le bon sens et/ou l'expérience - les faits suivants :
     I - compter, dénombrer, est une opération effectuée " très très " souvent dans la vie.
     II - le cerveau humain est particulièrement bien adapté à la détection des arrangements réguliers plan présentant deux " axes " principaux.
     III - le temps mis par le même cerveau humain à effectuer des actions " programmées " en mémoire procédurale est négligeable comparé à celui dépensé à exécuter une action " consciente "⁽¹⁷⁾
…
     Alors nous devons considérer que : la multiplication a été inventée par l'espèce humaine afin de " gagner du temps " lorsque l'on compte. Et donc pour libérer du temps bien utile à bien autre chose.⁽¹⁸⁾ Voilà donc comme promis, le " Pourquoi " de la multiplication. 

     Vous pressentez déjà - ou enfin ! c'est selon, suivant votre caractère … - la voie que nous nous apprêtons à emprunter. Lorsque nous avons ensemble entamé ce périple, très exactement à la page 1, je vous ai demandé de " compter " - maintenant il faudra plutôt employer le verbe dénombrer - Castor ou Pollux. Le résultat escompté est 42. Si l'on considère que chaque fois que votre regard, ou votre crayon, s'est posé sur un des points de Pollux vous avez dépensé une Unité de temps - Ut - alors Pollux ne vous a demandé que 6 + 7 = 13 Ut. Maintenant, si vous avez tenté de dénombrer Castor, par exemple pour vérifier que ma figure était bien " juste ", alors vous avez dépensé 42 Ut. Mais vous n'avez pas utilisé la multiplication puisque vous avez dénombré Castor point par point !…  

     Le fait désormais établi est que pour dénombrer le même nombre de points, 42, dans un cas on dépense 42 Ut alors qu'il suffit de 13 ut - plus de 3 fois moins - pour parvenir au même résultat. La suite du texte va vous exposer comment le mathématicien exploite ce fait. 

2- Les coûts de comptage des nombres entiers : 

     Les plus perspicaces d'entre vous toutes ⁽¹⁹⁾ auront remarqué que le " nombre " 42 ne s'arrange pas seulement en 6 lignes de 7 points comme Pollux nous le montre. C'est parfaitement vrai ! En fait il existe plusieurs façons d'arranger les points de Castor ou de Pollux de façon à les dénombrer. Je vous donne maintenant la méthode qui permet de trouver toutes les façons de trouver ces arrangements. Et à chaque nouvel arrangement trouvé nous calculerons les Ut qu'il nous faudrait dépenser pour dénombrer les nouveaux Pollux ainsi obtenus. 

     1 - On commence par imaginer les points de Pollux sur une seule ligne, donc 42 points à la " queue leu-leu " : on a bien 42 x 1 points, donc 42 ! OK… élémentaire.
     Maintenant combien d' Ut pour dénombrer ?… 42 ! Eh bien non ! J'ai fait exactement la même erreur autrefois lorsque j'ai " découvert " le 3ème crible. Et l'analyse de cette erreur m'a permis de trouver une idée très féconde pour la suite de mes recherches⁽²⁰⁾ . En fait il faut 1 Ut de plus lorsque l'on met les points en ligne. Vous ne vous en rendez pas compte mais votre cerveau à " mangé " 1 Ut pour constater que les points étaient alignés.
     2 - on essaie maintenant d'arranger Pollux sur 2 rangs. Voyons ! 42 = 2 x 21. Gagné ! on peut arranger en deux lignes de 21 points chacune. Combien d'Ut pour dénombrer maintenant ? Simple, nous l'avons déjà fait : 2 + 21 = 23. C'est bon.
     3 - on essaie avec 3. Alors sur 3 lignes çà va nous donner 3 x 14. Ne pas hésiter à s'aider avec des coquillettes !… Et le nombre d'Ut pour dénombrer 42 sera cette fois de 3 + 14 donc 17.
     4 - c'est au tour de 4. Bon on essaie pour voir si l'on peut trouver 4 lignes de points de " même longueur ". Eh bien là on ne peut pas. On arrive à 2 lignes de 11 points et deux lignes de 10 points. En effet, 42 n'est pas divisible par 4. Donc pas d'Ut ici.
     5 - pour 5 c'est encore plus simple ! on sait depuis l'école primaire que si 42 était divisible par 5, alors çà se terminerais par 0 ou par 5. Donc pas de Pollux qui aurait un côté de 5 points. Et par conséquent pas d'Ut.
     6 - pour 6… on l'a déjà fait et expliqué à la page précédente : 6 x 7 = 42, et le nombre d'Ut est 13.
     7 - pour 7, on remarque de suite que nous venons juste de procéder au calcul… Il est temps de s'arrêter.

 

⁽¹⁾Par courtoisie, je préfère toujours citer "ma lectrice" en premier lieu… cependant, l'écriture systématique de ",ou mon lecteur " étant à la longue fastidieuse, j'abrège dans la suite du texte cette locution convenue par ses initiales mises entre parenthèses : (oml). Mais la courtoisie n'est pas seule à dicter ce comportement qui présente l'avantage de " faire travailler " le féminin orthographique !…
⁽²⁾L'emploi de ce verbe n'est absolument pas innocent… patience, patience!…
⁽³⁾Les mathématiciens ont l'habitude de nommer les ensembles par des lettres seules comme " A " ou " B "… C'est assez triste au final !…et rendrait assez peu compte ici de la " gémellité " que je souhaite.
⁽⁴⁾Si ce n'est pas le cas, il est peut être temps de finalement consulter un ophtalmologiste…
⁽⁵⁾Essayez de ne pas accommoder votre vision sur le plan de la feuille.
⁽⁶⁾Ne me dites surtout pas que vous ne "voyez pas" duquel je parle!… sinon retournez à la note 4, ou laissez tomber cette lecture et entamez plutôt " L'homme qui prenait sa femme pour un chapeau " d'Oliver Sachs.
⁽⁷⁾Je suis désolé Mesdames et aimerais bien trouver un féminin pour ce mot là - vos congénères Iraniennes aussi sans doute ! - mais la seule substitution possible accordée par le Robert est " cervelle ", qui a malheureusement une connotation péjorative, et que je préfère en outre dorée au beurre avec un filet de citron… Si nous devions dîner ensemble, je me charge du citron.
⁽⁸⁾De sentir (avec ses 5 sens ici, et la vue est bien un des 5 sens…mais l'usage consacre " voir ").
⁽⁹⁾C'est tout de même plus joli que " Super-Phoenix " !… Maintenant à savoir qui de Super-Pollux ou de Super-Phoenix est le plus utile… En tous cas, je vous laisse deviner qui est le moins cher !…
⁽¹⁰⁾Oui… ici je veux exprimer que Super-Pollux est en quelque sorte constitué de points qui sont ses " enfants ", alors, avec 160 000 gosses ! … Si dans le lot un est plus " agité " que tous les autres, celles d'entre vous qui en ont [eu] plus de 2… pourrons dédouaner les sceptiques. Exception : celles d'entre vous qui possèdent le grade d'officier supérieur dans l'Armée Française… Si, si ! y'a même des Générales aujourd'hui.
⁽¹¹⁾Pour celles (ec) qui ont étudié les ondelettes, et particulièrement S. Mallat, le terme " multi-résolution " n'aurait-il pas finalement un pendant du genre " multi-détection " ( détection concourante à plusieurs niveaux d'échelles, par exemple ?!) .
⁽¹²⁾Rassurez vous!… si vous ne savez pas ce que tout cela illustre, LUI le sait et peut en causer des heures durant avec ses copains. Bon ! évitez de LE brancher là-dessus ou alors on arrivera pas à la fin avant de rendre visite à Morphée. Pour les plus malignes d'entre vous toutes, embrayez-le - justement ! - sur ce sujet aussi sensible que le genoux de Zizou, et pile-poil au moment du " … alors tu vois, la butée d'embrayage pousse le flasque… " achevez-Le d'un langoureux " Ouh là là ! Minou, toutes tes explications m'ont donné la migraine "…
⁽¹³⁾Les neuro-biologistes ont mis en évidence depuis longtemps les mécanismes intimes gérant ladite mémoire ainsi que le lieu où elle " réside " dans le cerveau.
⁽¹⁴⁾Si c'était celle de Mozart, j'aurais eu la délicatesse de mettre des majuscules!. Je sais, je tends à être familier de ci de là, mais j'ai un respect instinctif pour les Choses Eternelles…
⁽¹⁵⁾"Les Nombres" §2 p11, de H.-D Ebbinghaus et coll., Ed ; Vuibert 1998.
⁽¹⁶⁾Pour le cheval, la cause ne tient pas au fait qu'il ne sache pas nager - le cheval sait nager - mais bien plus au refus qu'oppose depuis toujours Mark Spitz de transformer son ranch texan en élevage de mustangs…
⁽¹⁷⁾Allez-y! essayez un peu de compter Castor en plein brouhaha, télévision en fond sonore, pleurs du petit dernier qui vient de tenter la face Nord du canapé à la " Frison-Roche " et Monsieur vous interpellant du fin fond des toilettes " Chérie ! y'a plus de papier !… tu veux bien m'en amener un rouleau du cellier mon Amour !… ". Un bon conseil… laissez le marner ; la prochaine fois IL y pensera avant !… Ben quoi ! vous êtes en train de faire des maths, Vous !
⁽¹⁸⁾A ce titre, je connais au moins une autre Grande Invention qui a obéit au même schéma : la machine à laver le linge… d'ailleurs en passant, Exercice-1 : " modifiez les hypothèses I, II et III afin de les adapter au lave-linge. Puis donnez la définition " fonctionnelle " du lave-linge "… Si vous galérez ! faites-vous aider par votre femme ! Elle au moins elle avait déjà fait le rapprochement !… Pffff…. Au fait, vous avez remis du papier ?!
⁽¹⁹⁾Donc une majorité!…
⁽²⁰⁾Pour les matheux : je ne me rendais pas compte qu'en fait l'alignement était " plongé " en 2D !… De cette erreur très embarrassante pendant 2 à 3 jours m'est venue l'idée d'explorer les comptages projectifs d'une " quantité " en toute dimension : sur chaque dim de l'espace dans lequel on " plonge " une quantité on procède à une " mesure projetée " et tout entier - et d'ailleurs tout autre réel aussi ! - peut être caractérisé de façon unique par le spectre des " mesures projetées " qu'il fournit. En plus, le produit de ces mesures est bien évidemment constant, et caractérise de façon unique la quantité. En parallèle au produit on définit une mesure de synthèse sur les mesures projectives - s-additivité quand tu nous tiens ! - et l'étude pour une quantité fixée des mesures de synthèse obtenues dans toutes les dimensions possibles - même non entières!…- nous fournit une " belle propriété " du Log Népérien : la " dimension " qui minimalise la mesure de synthèse d'une quantité !… Dès lors qu'on a créé un ensemble ordonné de quantités, un " nombre " peut être vu comme la mesure de synthèse en dimension 1 de la quantité associée. Par abus de langage le " nombre " devient La quantité qu'il représente, mais aussi un vecteur !… dès que l'on quitte la dim 1. Mais le plus important à mes yeux c'est que l'on parvient de la sorte à " découpler " - et peut-être même à inverser ! - l'ordre de construction des opérations arithmétiques. La " multiplication " peut être construite en parallèle à " l'addition ". Les deux en tous cas deviennent membres d'une même famille encore à préciser aujourd'hui, celle des " mesures de synthèse ". Un très très grand Merci à André Revuz qui a écrit : " mesurer […] reste encore mystérieux : on ne sait pas encore très clairement le sens qu'il faut donner au mot " mesurer " ". En ce qui me concerne, je déplace mes quantités dans les espaces et j'examine, évalue, compare leurs projections (mesurer = projeter ?), je suis géomètre de formation… Et merci L.Schwartz aussi !