|
L'identité
de Bézout géométrique
*
L'équation
de BEZOUT ax + by = 1 admet des solutions entières si et seulement a
et b sont premiers entre eux.
Nous allons travailler avec des nombres entiers positifs, aussi nous
allons modifier légèrement l'équation précédente
en :
Si
m et n sont deux nombres premiers entre eux
alors il existe deux entiers u et v tels que
m
v - n u = 1
L'algorithme
étendu d'Euclide permet de résoudre cette équation.
Voir aussi mon algorithme
d'Euclide.
Cependant, nous allons travailler sur un graphique dynamique afin
de mieux comprendre et visualiser les résultats.
Dans le plan quadrillé, appelons nœuds les points de coordonnées
entières,
soit O de coordonnées (0, 0) et
soit A un nœud de coordonnées (m, n) avec m et n premiers
entre eux.
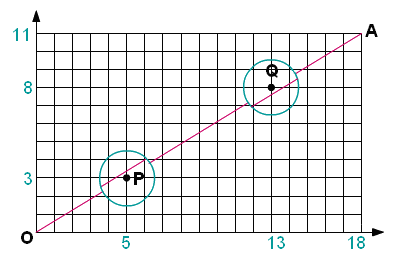
Sur l'exemple ci-dessous : m = 18 et n = 11 et nous avons A (18,
11).
Le point P de coordonnées (5, 3) est légèrement
au-dessous de [OA] et
le point Q de coordonnées (13, 8) est légèrement
au-dessus de [OA].
Nous pouvons constater que 18 x 3 - 11 x 5 = -1 et que 18 x 8 -
11 x 13 = 1.
Nous allons chercher de façon générale, parmi
tous les nœuds, quels sont les plus proches du segment [OA].
On note qu'il ne peut y avoir aucun nœud sur le segment [OA] autre
que les extrémités O et A (voir ma
page Vu pas vu ?).
On va constater que de façon générale pour
les points (u, v) les plus proches du segment OA, nous aurons
mv - nu = 1
ou
mv - nu = -1

Animation
dans le rectangle
Choisir avec les flèches les deux entiers m et n désirés.
Ensuite, il est possible de déplacer très doucement
la droite avec un léger halo (parallèle
au segment [OA]) .
Noter alors l'évolution de l'équation de la droite
et les points donnant des valeurs entières.
On peut cacher cette droite en cliquant le bouton adéquat.
Cliquer chaque nœud pour obtenir la valeur de mv - nu en
ce point de coordonnées (u, v).
CLIQUER

Comprendre
avec le parallélogramme et l'animation
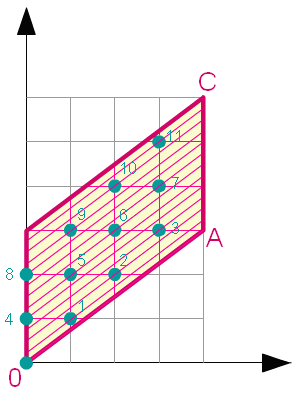
Dans l'exemple ci-dessous, m = 4 et n = 3.
Choisissons
A de coordonnées (m, n) ;
C de coordonnées (m, 2n) ;
B de coordonnées (0, n).
Construisons le parallélogramme ABCD.
Pour un point M de coordonnées (x, y) du plan, appelons b(M)
le nombre my - nx (dans le cas présent,
4y - 3x).
Nous constatons que dans le parallélogramme privé de
ses bords [AC] et [BC], la fonction b prend
des valeurs entières de 0 à mn -1.
En traçant les parallèles à la droite (OA) passant
par les nœuds, nous constatons que b prend
toutes les valeurs consécutives de 0 à mn -1.
Nous obtenons ainsi les droites d'équation : my - nx = b.
Vérifier ces résultats dans différents cas, sur
l'animation ci-dessous.
Je proposerai quelques explications ensuite.
Quelques explications
Quelles
que soient les valeurs des deux entiers m et de n, premiers entre
eux,
nous savons que
-la
droite (OA) a pour équation 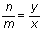
c'est à dire
my - nx = 0 ;
-les parallèles à (OA) ont
pour équation
my - nx = b
;
-qu'en faisant glisser vers le "haut"
chaque droite d'équation
my - nx = b ,
b prend des valeurs
strictement croissantes ;
Montrons
que
sur chaque segment parallèle à (OA) construit sur
un nœud, dans le parallélogramme (sans les bords [AC] et
[BC]), le nœud est unique..
Remarquons que dans la page
Vu pas vu
? nous avons déjà donné
une explication de ce résultat.
Supposons qu'il existe dans le parallélogramme,
deux points M(x, y) et N(x', y')
à coordonnées entières ayant la même
valeur de b,
sur le même segment.
Alors
my - nx = my' -nx'
m (y - y') = n ( x - x')
ou
(1)  =
=
M et N sont contenus dans le parallélogramme et sur le
même segment parallèle à (OA),
donc
(x-x') < m
et
(y-y') < n.
L'équation
(1)
signifie que  serait une écriture simplifiée de la fraction
serait une écriture simplifiée de la fraction  . .
Or ce n'est pas possible. En effet, m et n sont deux nombres premiers
entre eux, la fraction m/n est donc irréductible.
Les points M et N sont donc identiques.
Chaque segment parallèle à (OA) passant par un
nœud, ne passe par aucun autre nœud.
Finalement,
dans le parallélogramme,
- sur chaque segment, il y a au plus
un nœud donnant une valeur entière de b
;
- deux nœuds différents ont forcément
des valeurs entières différentes
(puisqu'ils ne peuvent
être sur le même segment et
qu'en "montant"
une droite prend des valeurs b strictement
croissantes) ;
- en excluant les bords [AC] et [BC], le parallélogramme
contient exactement mn nœuds ;
- la plus petite valeur d'un nœud est
0 soit b(O) = m*0 - n*0 = 0 ;
- la plus grande valeur d'un nœud est
inférieure à mn
(
valeur obtenue sur le segment [BC] (le plus "haut")
exclu avec b(B) =
m*n - n*0 = mn) ;
Nous avons donc mn valeurs entières différentes
allant de 0 à mn - 1.
Il y a mn nœuds prenant des valeurs entières toutes
différentes.
On en conclut que les mn nœuds prennent chacun une valeur
différente de 0 à mn - 1.
Chaque valeur entière de 1 à mn - 1, est ainsi prise
une et une seule fois en un nœud du parallélogramme.
En particulier, la
valeur 1 est obtenue au nœud le plus proche du segment [OA].
Ce nœud est unique dans le parallélogramme.
Nous venons de trouver une illustration graphique de l'identité
de Bézout.
Nous
obtiendrions exactement le même raisonnement pour le nœud correspondant
à la valeur négative -1.
Autres résultats
Lorsque deux nombres sont premiers
Si PGCD (a, b) = c Alors, il existe 2 entiers relatifs x et
y (positifs ou négatifs) tels que ax + by = c
EGALITE DE BEZOUT
Soient a et b deux entiers relatifs non nuls et d leur PGCD.
Il existe deux entiers relatifs u et v vérifiant l'égalité de BEZOUT
au + bv = d.
THEOREME DE BEZOUT GENERALISATION
L'équation de BEZOUT ax + by = c ( c entier fixé non nul) admet des
solutions entières si et seulement si c est un multiple de d (d étant
le PGCD de a et de b)
THEOREME DE GAUSS Si un nombre a divise un produit de facteurs
et si a est premier avec l'un des deux facteurs alors a divise le
deuxième facteur.
Pour en savoir plus, sur le théorème de Bezout :
http://fr.wikipedia.org/wiki/Identit%C3%A9_de_B%C3%A9zout
*
sur une bonne idée de Pierre Jullien
|



