Le problème

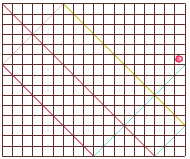
Prenons un billard rectangulaire dont le plan est quadrillé avec des carrés. Par exemple un billard de 18 cases sur 15. Une balle part du coin gauche en haut ; elle rebondit sur les bords. Combien de cases traversera-t-elle avant de ressortir par un autre coin ? Et avec un billard de 840 cases sur 154 ?

Ci-dessous entrez les nombres de lignes et de colonnes.
Pour des raisons pratiques, le nombre de lignes ou de colonnes sera plus petit que 19. 
Faire varier ces nombres de cases et observer le trajet suivi par la balle sur le billard.
Noter le résultat et conjecturer.

CLIQUER

On déplie et on replie

Ci dessous, un billard de 4 cases sur 6 cases (remarque : le plus petit multiple commun de 4 et de 6 est 12).
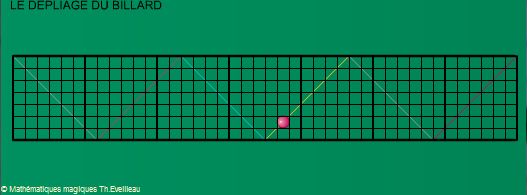
La balle est lancée sur ce billard. On déplie alors avec des symétries d'axe vertical.
Cela revient à juxtaposer trois exemplaires du billard nous donnant un rectangle de 12 cases sur 6.
On imagine alors le parcours de la balle dans ce billard déplié puis on replie les trois exemplaires du billard.
Cette façon de procéder peut nous faire entrevoir le résultat général.

CLIQUER

Résultat et explication

Il s'agit d'une application du plus petit multiple commun à deux nombres.
Ci-dessous choisir le nombre de lignes plus petit que 8, de même pour le nombre de colonnes.
Le billard est recopié en plusieurs exemplaires accolés.
Ce procédé permet de bien comprendre le trajet et les rebondissements de la balle.
En observant le trajet de la balle, on se rend compte que le nombre de cases traversées doit être à la fois un multiple du nombre de lignes et du nombre de colonnes pour que la balle puisse ressortir par un coin du billard.

CLIQUER

---