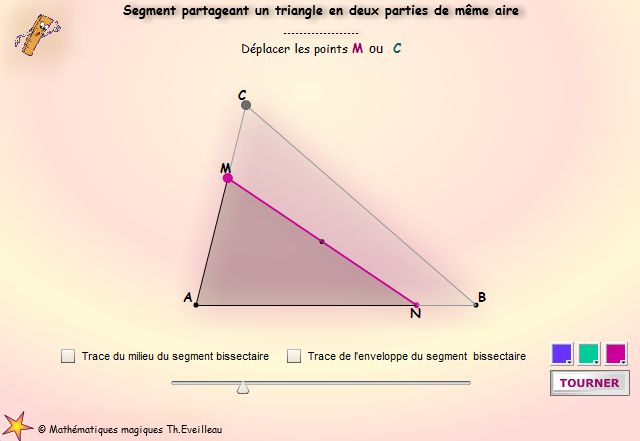
Les segments partageant le triangle ABC en deux parties de même
aire ont comme enveloppe une sorte d'étoile composée
de trois arcs d'hyperbole.
Démonstration
ICI
Voir également le site de
Diophante pour plus de solutions.
 Segments
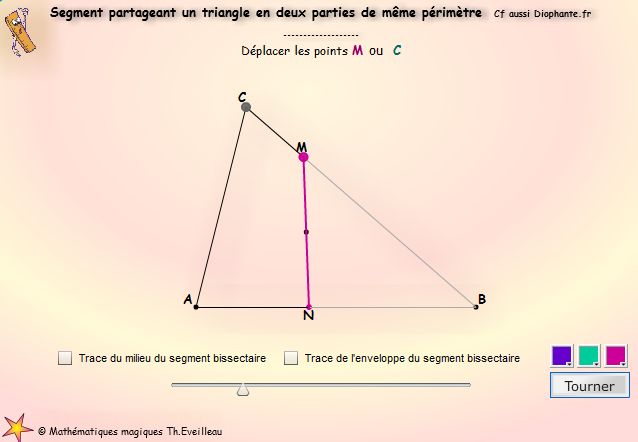
partageant un triangle en deux parties de même périmètre
Le
point M parcourt le périmètre
du triangle, le déplacer avec les flèches du clavier
ou avec la souris.
Il est à l'origine d'un segment partageant le triangle ABC
en deux parties ayant le même périmètre.
On
peut aussi déplacer le point C.
Dans
l'animation suivante,
-On peut déplacer le point M
autour du triangle ABC, ou le point C,
à la main avec la souris ou au clavier .
Alors la position du point N est automatiquement
calculée et mise à jour.
-On peut également déplacer le sommet C
du triangle.
Dans ce cas, les traces sont réinitialisées.
-Cliquer
les boutons adéquats pour visualiser les traces du milieu du
segment de partage ou bien l'enveloppe de ce segment.
Solution et démonstration ICI
Voir également le site de
Diophante pour plus de solutions.
CLIQUER
Segments
partageant un triangle en deux parties de même aire et de même
périmètre
Cette
fois il faut essayer de trouver la position du point M,
déterminant une ligne qui coupe le triangle à la fois
en deux parties de même périmètre et de même
aire.
La ligne dessinée partage d'emblée le triangle en deux
parties de même périmètre,
à vous de jouer pour obtenir des aires identiques.
En déplaçant
doucement le point M sur le périmètre du triangle,
ou bien en lançant l'animation avec une petite vitesse,
on peut observer que lorsque le segment bissecteur du périmètre
passe par le centre du cercle inscrit,
il partage également le triangle en deux parties de même
aire.
La démonstration géométrique qui suit est très
simple.
Démontrons
géométriquement que :
1°) cette condition est suffisante
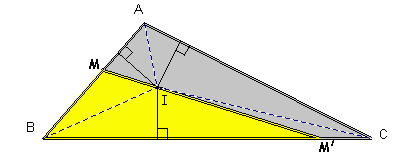
Appelons p le demi périmètre du triangle ABC.
Appelons
I, le centre du cercle inscrit au triangle.
Soit r son rayon.
Pour calculer l'aire du triangle MBM', il suffit de le découper
en deux triangles BIM' et BIM.
BIM' a pour aire BM' * r/2
et BIM a pour aire BM * r /2
La
somme des aires de ces deux triangles est donc (BM +BM') * r /2
soit p * r/2.
On ferait la même chose avec le polygone MACM' en le découpant
en trois triangles :
MIA d'aire MA* r/2
AIC d'aire AC * r/2 et enfin
ICM' d'aire M'C * r/2
Comme [MM']
partage le périmètre
en deux parties de même longueur
le polygone MACM' a pour aire également p * r/2.
Ce raisonnement reste valable quel que soit le triangle ABC.
Quand [MM'], bissecteur de périmètre, passe par
Ie centre du cercle inscrit à ABC,
le triangle est bien partagé en deux parties de même
aire.
De même on montrerait que
Quand [MM'], bissecteur de l'aire, passe par Ie centre du cercle inscrit
à ABC,
le triangle est bien partagé en deux parties de même
périmètre.
Remarque
:
on retrouve ainsi la formule donnant l'aire du triangle :
Périmètre * rayon cercle
inscrit
2°) cette condition est nécessaire
Rappel
L'aire d'un triangle est égale au demi périmètre
multiplié par le rayon du cercle inscrit.
Supposons un segment [MM'] dans le triangle à la fois
bissecteur de l'aire et du périmètre.
Prenons encore p pour demi périmètre de ABC
et r comme rayon du cercle inscrit.
L'aire de chacune des deux parties est ainsi égale à
p * r/2.
Le tour de chaque partie est donc p (en ne comptant
pas MM').
MM' découpe toujours le triangle en un triangle et un quadrilatère
ou en deux triangles.
Supposons que [MM']
ne passe par
I centre du cercle inscrit.
Nécessairement le point I se trouve soit dans le triangle
soit dans le quadrilatère.
En effet, I est toujours à l'intérieur du triangle
ABC.
Exemple de figure les longueurs vertes et roses sont supposées
identiques
Quel que soit le polygone (triangle ou quadrilatère) contenant
I dans le triangle,
le calcul de son aire après découpage en triangles
autour du point
I ,
mène au résultat :
p
* r/2 + Aire (MIM').
Nécessairement on obtient Aire (MIM') = 0 et
donc I est situé sur [MM']
CQFD.
.
|
