|
Une jauge pour une
cuve cylindrique couchée et autres cuves...
Autres
cas
Les cuves du chai de
Norbert,
et l' oblique.
La cuve de Phil
 Le
problème
Claude possède une cuve de
forme cylindrique contenant le fuel avec lequel il chauffe sa maison.
Sa cuve mesure 2,65m de longueur et a un diamètre de 1,20m.
Régulièrement il fait le plein... Mais auparavant il
aimerait savoir combien il lui reste de fuel dans la cuve
(ne serait-ce que pour vérifier sa facture).
Aussi voudrait-il construire une jauge. Il désire une graduation
tous les 10 cm lui fournissant la
quantité de fuel contenue dans la cuve.
Comment procéder ?
Notons
que pour une cuve cylindrique verticale, le problème
est très simple.
Il suffit de multiplier la surface du disque de base par la
hauteur du liquide dans la cuve.
Afin de faciliter la vérification, la petite animation
suivante vous donne directement le résultat.
Cliquer
Simulation
pour la cuve couchée
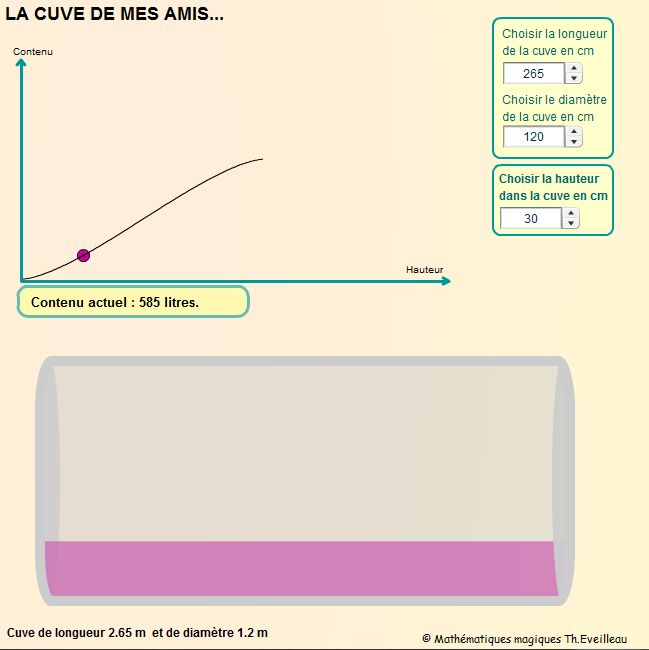
Ci-dessous cliquer sur les flèches
pour fixer d'abord la longueur et le diamètre de la cuve.
La courbe donnant la capacité de la cuve en fonction de la
hauteur de remplissage est mise
à jour au fur et à mesure des changements de mesure
de la cuve.
Choisir
ensuite la hauteur désirée en cm (cette hauteur correspond
à la partie trempée de la jauge).
La cuve se remplit alors correctement et un gros point se déplace
sur la courbe pour indiquer la
capacité qui est affichée en litres.
ATTENTION, si vous entrez vos valeurs au
clavier,
appuyez ensuite la touche ENTREE pour valider chaque donnée,
vérifiez l'affichage des valeurs prises en compte.
Cliquer
L'animation
simplifiée ci-dessous donne les résultats avec
des dimensions éventuellement plus grandes.
Cliquer
ATTENTION,
si vous entrez vos valeurs au clavier,
appuyez surtout la touche ENTREE pour valider chaque donnée,
vérifiez l'affichage des valeurs prises en compte.
Explication
et calculs
 |
Il
s'agit de calculer le volume d'un solide dont la base correspond
à la partie rouge de la figure ci-contre et de longueur
2,65m.
Les mesures étant indiquées en mètres,
posons
R, le rayon de la cuve
et L sa longueur.
Dans
le cas où la hauteur est inférieure au rayon,
nous pouvons
chercher la surface de la partie rouge c'est à dire
celle du secteur angulaire SOA moins celle du triangle rectangle
SOH.
Nous avons cos β= 
.
L'angle
β est donc l'angle dont le cosinus est .
C'est β = Arc cos()
( β est exprimé en radians ci-dessous.)
On peut le déterminer en utilisant une table de trigonométrie
ou une calculatrice.
|
Aire(SOH) =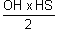 
Aire(SOH) =R² 
= R² 
β est exprimé en radians d'où
:
Aire
(secteur SOA) = 
= 
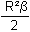
Finalement
Aire(SHA) =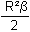
- R²
=  .
L'aire de la partie rouge est le double de celle de SHA soit :
.
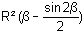Le volume est
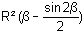L .
Pour
obtenir le volume en litres, il suffit de convertir les longueurs
en dm, puisque 1dm3 correspond à 1 litre.
En dm, le rayon est 10R et la longueur 10L.
Avec β = Arc cos()
, la capacité en rouge de la cuve est en litres :
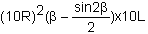
Dans le cas particulier ci-dessus avec un rayon de 0,6m et une
longueur de 2,65m,
cela donne : 
Dans le cas où la hauteur est supérieure ou égale
au rayon,
la formule trouvée précédemment donne également
l'expression du volume
car le signe des lignes trigonométriques change et permet
de retrouver le bon résultat :
le triangle enlevé ci-dessus, s'ajoutera correctement.
Pour ceux qui ne sont pas totalement convaincus, il suffit, lorsque
la capacité est
supérieure à la moitié de la cuve, d'utiliser
la symétrie de la figure.
Par exemple, pour une hauteur de liquide égale au diamètre
moins h avec (h<R), il suffit de calculer
le volume de la cuve pleine
moins
celui qu'on obtient pour une hauteur h de
liquide.
En vérifiant les résultats obtenus, on observe très
bien cette symétrie.
Joël
propose la démonstration complète utilisant cette
symétrie ICI.
|