Les lapins de Fibonacci... (1)

         Applications        


La version ancienne est ici 

 

 

Voici le problème des lapins de Fibonacci qui fut proposé en 1202 :

Partant d'un couple, combien de couples de lapins obtiendrons-nous après un nombre donné de mois sachant que chaque couple produit chaque mois un nouveau couple, lequel ne devient productif qu'après deux mois.

 

CLIQUER  

Chaque mois, le nombre de lapins est la somme des nombres des 2 mois précédents :
- nombre de lapins existant (du mois précédent )
- nombre de bébés des lapins qui ont au moins deux mois.

La suite des nombres de lapins est appelée suite de Fibonacci.

La croissance de cette suite est de nature exponentielle.
A partir d'un certain rang, elle est aujourd'hui considérée comme "presque géométrique" avec une raison égale au nombre d'or :
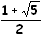soit environ 1,618. En effet, le rapport de deux termes consécutifs tend vers ce nombre d'or.
Ce problème des lapins est remarquable en ce qu'il constitue certainement la première modélisation démographique réaliste de l'histoire avec des données assez cohérentes avec la biologie.
Pour Fibonacci il s'agissait avant tout d'une récréation mathématique. Il ignorait certainement le nombre d'or.

 

CLIQUER  

   

Applications

Au bout de combien de mois aura-t-on 4181 couples de lapins, puis 6765 couples de lapins ?           (2)

Leonardo monte un escalier. A chacun de ses pas, il franchit soit une, soit deux marches.
De combien de manières différentes peut-on monter un escalier de 6 marches ? (3)

Prenons un exemple réel, cette fois-ci : le cœur de certaines fleurs, les écailles d'un ananas ou d'une pomme de pin forment deux familles de spirales enroulées en sens inverse.
Sur une pomme de pin, vous compterez 5 spirales dans un sens et 8 dans l'autre, sur l'ananas, 8 et 13, sur la fleur de tournesol 21 et 34.
Chaque fois, nous obtenons des nombres de Fibonacci !
Pas de mystère : la croissance de ces fleurs ou de ces fruits obéit à un principe de construction rigoureux, et celui-ci est lié à la suite de Fibonacci.  

 Pour en savoir plus sur le nombre d'or
cliquer ici
 

 

(2) 18 mois puis 19 mois. 

(3) Il y a trois façons de monter un escalier de trois marches. Pour 6 marches il y a 13 manières...
Pour un nombre quelconque de marches, on vient soit du niveau précédent, soit de deux niveaux en dessous.
Il faut donc additionner les nombres de manières de monter à chacun de ces niveaux, comme dans la suite de Fibonacci..