Pierre Jullien,
vous offre ici de grandes opérations interactives réalisées
avec un tableur...
|
Multiplication
per gelosia 
La multiplication per gelosia
Ancienne version javascript ICII
ENTRER LES DEUX NOMBRES A MULTIPLIER
dans l'animation ci-dessous puis cliquer l'un des boutons VOIR ou FAIRE.
Le choix VOIR lance le calcul automatique tandis que
FAIRE permet de s'exercer : après avoir entré les nombres dans les cases blanches adéquates, il faudra cliquer sur OK.
Chaque case erronée sera effacée et les erreurs seront comptabilisées jusqu'à réussite...
CLIQUER
Cette merveilleuse technique nommée aussi italienne ou grecque qui nous vient d'Orient est utilisée au XVème siècle par le mathématicien arabe Al kasi,.
Mais on la trouve beaucoup plus tôt chez les arabes aux alentours du XIIIe siècle (multiplication par le quadrillage ou par le tableau).
Elle serait dans un ouvrage de Fibonacci de 1202.
Ainsi, elle est présente à des périodes différentes en Chine, en Inde, dans les pays d'Islam et en Europe.
Elle a porté des noms divers : "par filet", "par grillage" puis à la fin du Moyen-Age la technique fut surnommée "per gelosia".
Ce nom "per gelosia" fait allusion à la pièce en bois qui équipait certaines "fenêtres à jalousie" en Italie chez les maris jaloux.
Ils acceptaient que leur femme regarde ce qui se passe dans la rue, mais les hommes ne devaient pas pouvoir la voir.
Ci-dessous, des fenêtres à jalousie que j'ai photographiées à Ajaccio en mai 2016.
Cette technique a fini par donner notre algorithme de multiplication.
Dans chaque case on note le produit du nombre de la première ligne par celui correspondant dans la colonne de droite. Il suffit de bien connaître ses tables.
Pour le résultat final, on ajoute en DIAGONALE en tenant compte des retenues additives, les résultats obtenus dans les cases et ceci de droite à gauche.
Les diagonales sont marquées par les traits obliques coupant les cases en deux.
Bien entendu on ne prend ni la première ligne ni la colonne de droite contenant les nombres de départ.
Elle présente de nombreux avantages :
Le tracé des lignes peut se faire à main levée. Et si l'on se trompe, on retrouve très vite l'erreur. On voit également sans problème si l'erreur est due au manque de connaissance des tables ou à une méconnaissance de l'algorithme.
Vous avez été très nombreux à m'envoyer une vidéo de plus de deux mégas octets...
où l'on voit une multiplication avec des tracés de lignes : la voici ICI.
Même technique avec cercles au lieu de lignes : ICI
Cette technique amusante ne fait apparemment intervenir aucune table de multiplication.
Beaucoup se demandent si la technique est généralisable.
La réponse est OUI.
Voici une animation de cette technique. Elle montre le lien direct de cette technique avec la grecque.
Il suffit d'entrer deux nombres et d'observer les tracés et comptages, pour s'en persuader.
On trace horizontalement et verticalement le nombre de lignes ou de colonnes correspondant au chiffre indiqué en haut ou à droite.
Ensuite comme pour la technique à la grecque, il suffit de compter les points en diagonale.
Les retenues éventuelles sont reportées sur la diagonale de gauche.
En comptant le nombre de croix d'un rectangle de n lignes sur m colonnes,
on redéfinit tout simplement la multiplication n x m.
CLIQUER
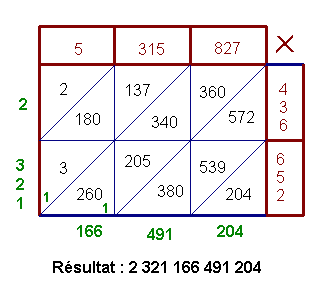
Cherchons par exemple le résultat exact de 5 315 827 x 436 652
Si nous prenons une calculette nous obtenons un résultat écrit avec la notation scientifique ce qui ne nous convient pas toujours. Cependant il n'est pas très agréable d'effectuer l'opération manuellement.
La multiplication précédente nous permet de simplifier le calcul. Il suffit de grouper les chiffres par 3 comme ci-dessous, chaque calcul intermédiaire peut être effectué à la machine. Il ne reste plus alors qu'à effectuer l'addition finale en diagonale.
De fait le calcul est effectué en base mille.
Pierre Jullien, vous offre ici de grandes opérations interactives réalisées avec un tableur...
Grandes multiplications en base mille
Grandes divisions en base dix mille.
Ancienne version javascript ici
