Pavages non périodiques

Les pavages non périodiques sont ceux dans lesquels il n'existe pas de motif minimal qui permette de revêtir toute la surface par déplacement.
Jusqu'aux années 1960 et 1970, cela constitua un défi pour la pensée mathématique.

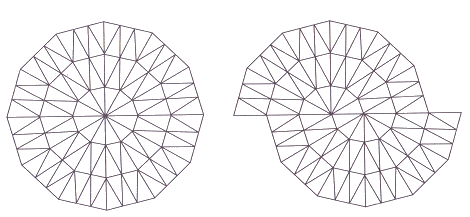
Par exemple ci-dessous, à gauche un pavage construit avec un triangle isocèle.
On coupe le dessin en deux et l'on déplace la moitié supérieure vers la gauche, on obtient un revêtement spiral non périodique.


Cependant le vrai défi fut de construire un ensemble de tuiles qui ne donnerait que des pavages non périodiques.

Les 17 types de pavage du plan étaient connus quand Penrose s'intéressa aux pavages non périodiques dans un but de divertissement mathématique.

E n 1984, on découvrit des matériaux présentant une structure fortement ordonnée comme celle des cristaux mais non périodique : les quasi-cristaux.
Les pavages non périodiques, en particulier ceux de Sir Roger Penrose (né en 1931) s'avérèrent alors un modèle plausible de ces étranges matériaux.
Ils sont dits quasi-périodiques, tout motif apparaissant dans le pavage réapparaît régulièrement.
Plus généralement toute portion finie du pavage, aussi grande soit-elle, se répète infiniment dans le pavage.

Les pavages de Penrose peuvent tous être construits à partir d'une d'une paire de triangles d'or.
Le pavage de base type P0 est construit uniquement avec des triangles d'or.

Il existe plusieurs types présentant de nombreuses variantes :

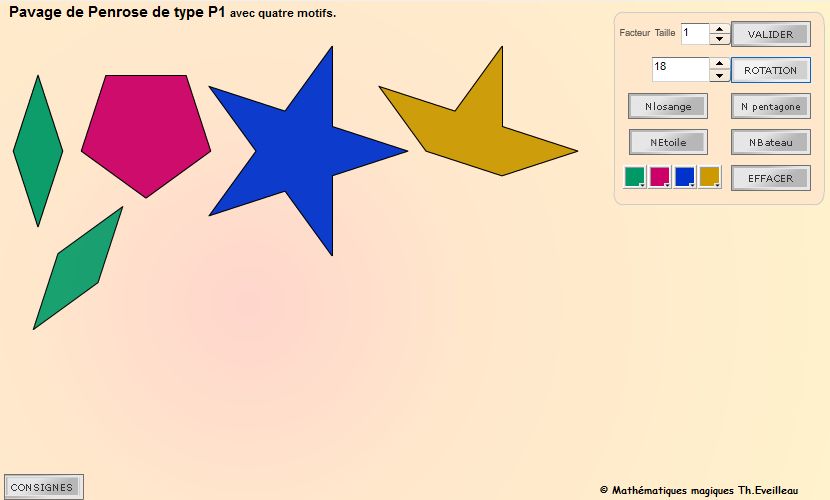
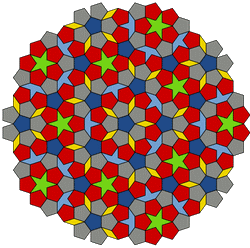
- le type P1 utilise des pentagones, des losanges, des pentagrammes et des portions de pentagramme ;

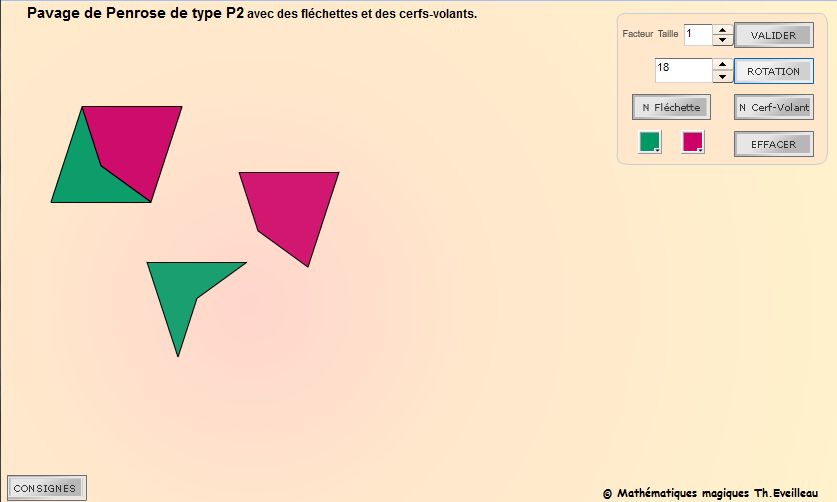
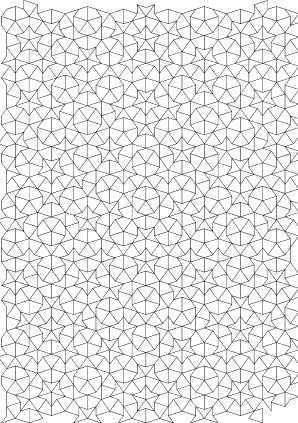
- le type P2 utilise des fléchettes et des cerf-volants : ce sont deux quadrilatères, l'un concave et l'autre convexe. On démontre dans ce pavage que le rapport entre le nombre de cerfs-volants et de fléchettes tend vers le nombre d'or φ.

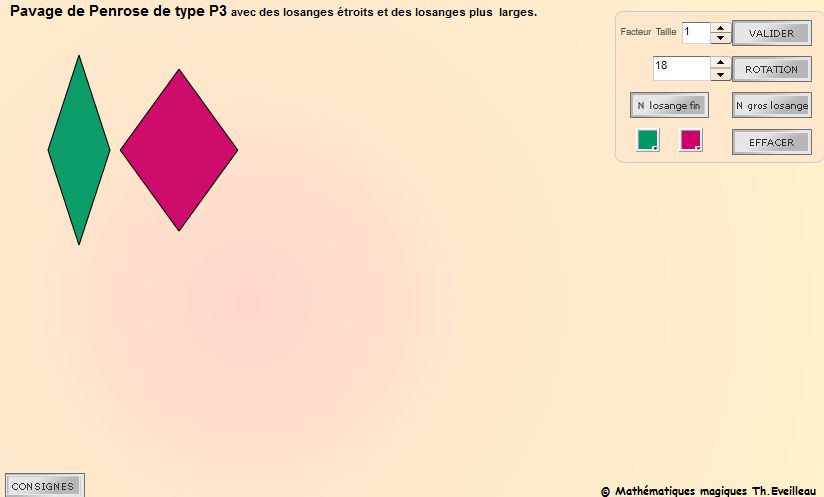
- le type P3 utilise des losanges : des fins et des plus larges.

Ces pavages présentent une symétrie d'ordre 5 (invariance par rotation d'angle 2π/5 radian, soit 72 degrés).

Exemples de pavages non périodiques pouvant être construits avec les fléchettes et cerf-volants de Penrose :

Mosaïque Roue de carosse

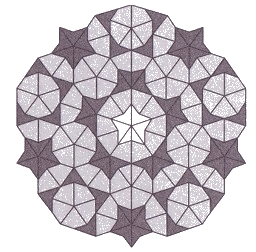
Mosaïque Etoile

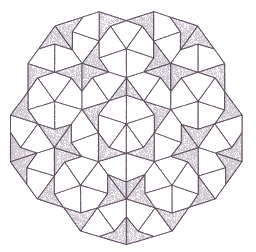
Mosaïque Soleil

Construction à la règle et au compas de la fléchette et du cerf-volant
à partir d'un pentagone régulier

Voici, pas à pas à la règle et au compas, la construction rigoureuse d' une fléchette et d'un cerf-volant en partant dun pentagone régulier.

CLIQUER

Jouons, expérimentons et essayons de construire un pavage de Penrose b

Pavage de Penrose de type P2 : fléchettes et cerfs-volants.

Poser la souris sur le bouton CONSIGNES à gauche en bas de l'animation pour plus d'indications.
Poiur s'aider d'un exemple, on peut utilisernPoser la souris sur le bouton CONSIGNES à gauche en bas de l'animation pour plus d'indications.
Pour s'aider d'un exemple, on peut utiliser la grille suivante ICI.