ROTATION
(Voir
aussi la page Rotations dynamiques)
Les bords du calque ne sont pas parallèles à
ceux de l'original.
Sur l'animation, nous constatons
- qu'une droite a pour image une droite qui ne lui est pas parallèle
;
- il existe un point qui est sa propre image ;
- les points d'intersection des droites parallèles avec leurs
images respectives sont alignés ; cet alignement dépend
de la direction des parallèles tracées sur l'original.
Le calque étant immobilisé sur l'original, c'est aussi
vrai pour les bords de la feuille.
Une droite étant déterminée par deux points,
il nous suffit, pour obtenir les droites d'alignement, de prendre
chaque fois l'intersection d'un bord et de son image.
Ces deux droites se coupent en un point, dont nous constatons qu'il
est sa propre image. Ce point est INVARIANT.
Démontrons que ce point est le centre de la rotation.
Le rectangle rose représente la feuille originale et le bleu
représente le calque.
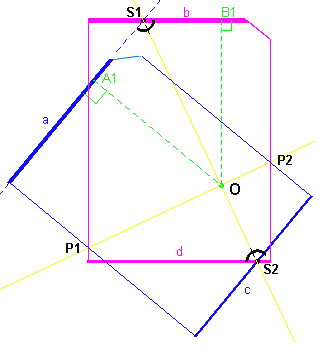Soit O le centre de rotation transformant l'original rose en
la copie bleue.
Traçons les deux perpendiculaires menées de O sur les deux
segments a et b.
B1 est l'image de A1 dans la rotation de centre O
:
- il est sur le segment b image de a et
- sur la perpendiculaire (OB1) image de la perpendiculaire
(OA1) à a.
Nous avons donc OA1=OB1.
Nous en déduisons*1 que O
est sur la bissectrice de l'angle marqué en S1. La bissectrice
est donc la (OS1).
De même on démontrerait que (OS2) est la bissectrice de l'angle
marqué en S2. Ces deux bissectrices sont parallèles car elles
sont bissectrices de deux angles ayant des côtés parallèles deux à
deux.
Ces deux bissectrices parallèles ont un point commun O, elles sont
donc confondues en la droite (S1S2) *2.
Cela revient à dire que le centre de rotation est situé sur la droite
(S1S2).
On démontrerait de la même façon que O
est situé sur la droite (P1P2).
O est donc à l'intersection des deux droites (S1S2) et (P1P2).
*1 car tous les points de la bissectrice
d'un angle sont équidistants des côtés de cet angle.
*2 ceci explique pourquoi les points d'intersection
des droites parallèles et de leurs images sont alignés : ils sont
situés sur la bissectrice de l'angle formé par chaque parallèle avec
son image.
Au lieu de prendre une feuille, nous aurions pu prendre toute partie
du plan voire le plan lui-même.
Le centre de rotation peut être quelconque voire à l'extérieur
de la feuille.
C'est le cas dans l'animation suivante.
CLIQUER
Avec un centre de rotation extérieur à
la feuille.
SYMÉTRIE
orthogonale
Marquons sur l'original deux points u et v; retournons
le calque et appliquons le sur l'original de sorte que l'image de
u soit en u et celle de v en v. C'est
ce que nous effectuons sur l'animation ci-dessous.
Nous constatons que tous les points de la droite (uv) sont
invariants. ce sont les seuls. Pour tout autre point m, la droite
(uv) est la médiatrice du segment (mm') où
m' est le point du calque image de m.
La transformation est la SYMETRIE ORTHOGONALE d'axe (uv).
Si nous retournons le calque à nouveau, en maintenant
l'image de u en u et celle de v en v
alors nous faisons coïncider le calque avec l'original.
Autrement dit, composer une symétrie avec elle-même,
c'est effectuer la transformation IDENTITE (tout point est
sa propre image).
VISSAGE
Maintenant plaçons le calque retourné sur
l'original sans nous préoccuper de faire coïncider des
points quelconques.
Nous constatons que les points d'intersection des droites parallèles
avec leurs images sont alignés sur une droite (D).
La droite (D) varie avec la direction des parallèles
de l'original. (D) a cependant une direction précise
: celle de la bissectrice des directions d'une droite et de son image.
Matérialisons avec un deuxième calque la symétrie
orthogonale d'axe (D) qui transforme alors le plan du premier
calque en un plan (P).
(P) se déduit du plan original par une translation.
Finalement pour obtenir la transformation complète, nous pouvons
opérer en deux temps :
- amener le plan original, par une translation sur le plan
du deuxième calque ;
- amener le plan du deuxième calque, par une symétrie
orthogonale, sur le plan du premier calque.
La nouvelle transformation que nous venons d'effectuer s'appelle un
VISSAGE. Le plus souvent, il n'y a aucun point invariant, sauf
dans le cas des symétries orthogonales, qui sont des vissages
particuliers (avec un vecteur de longueur nulle).
