| Mesurer
la largeur d'une rivière
sans se mouiller
 Instrument
de Gerbert
Bâtons
différents
Bâtons
pareils
Rivière
avec Errard
Biblio
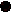 Avec
l'instrument d'Errard
| Il
est constitué de deux bâtons "articulés" AK
et AC ayant
un frottement suffisant pour qu'ils gardent un angle déterminé
au cours de la mesure.
Cet instrument sert à mesurer une distance horizontale
(ici la largeur KB
de la rivière dont l'extrémité
B est inaccessible.
L'observateur est
placé au bord de la rivière en K (œil
verticalement en A).
Il positionne la branche AK
verticalement et la branche AC de
façon à viser
de A,
le
bord B
de la
rivière.
Ceci détermine l'angle de l'instrument en A. |
 |
On
fait ensuite pivoter l'instrument sans changer son
angle A,
autour de la verticale (AK)
On vise ainsi un point B'.
Ce
point permet de déterminer la distance KB'
sur la terre ferme.
La distance inaccessible KB
est égale à cette distance mesurable KB'.
Dans
l'animation suivante
On
peut déplacer les points A,
B
et
C
avec
la SOURIS ou au CLAVIER.
Pour cela, on déplace le dernier point sélectionné
avec les flèches DROITE, GAUCHE, HAUT et BAS.
Les quatre flèches pour C,
Haut et Bas pour A.
Gauche et Droite pour B.
ATTENTION
c'est très précis, commencer avec la souris et continuer
avec le clavier pour plus de précision.
Quand la position est correcte, un petit bip et un message
le signalent. Alors l'instrument fait un demi-tour.
CLIQUER
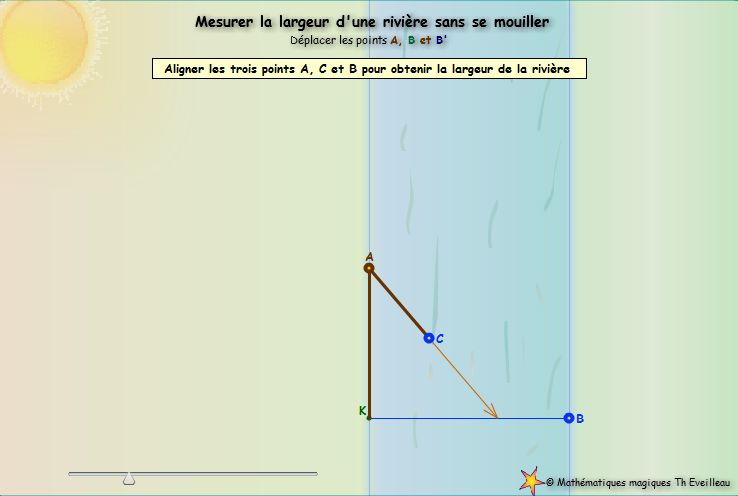La
bonne position est obtenue quand les points A,
C et B sont alignés.
Alors KB
= KB'
| La
largeur de la rivière est KB'. |
On
peut également dessiner à l'échelle sur feuille
le segment AK et reporter avec un gabarit
l'angle A,
ou bien redessiner le triangle rectangle AKB',
dont on connaît AK et les angles en
A et B'.
Autre
solution :
| Sur
le sommet C d'un bâton placé verticalement en
A, on dispose une équerre de telle sorte que la direction
de l'une des branches passe par B.
Soit
D le point où la direction de l'autre branche rencontre
le sol horizontal.
Le
triangle rectangle en C, DCB donne :
AB = ( AC 2 / AD) |
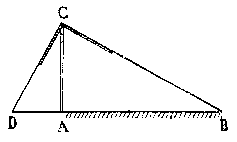
AB: largeur de
la rivière |
ERRARD
DE BAR-LE-DUC.
|