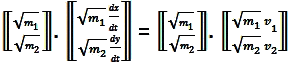Quand
des blocs calculent précisément un nombre mystérieux...
Le
problème
Animation pour expérimenter
Réponses
Première explication scientifique
Changement de point de vue avec le trajet d'un rayon lumineux
. Collisions
sur une droite
. Vers
le rayon lumineux
. Réflexions d'un rayon lumineux entre deux miroirs
.Démonstration de l'égalité incidence et réflexion
Autres expériences autour du nombre π
Question subsidiaire
Le
problème
Retrouvez ce problème G2942
chez Diophante
ici :
http://www.diophante.fr/problemes-par-themes/g-probabilites/g2-combinatoire-denombrements/4469-g2942-gulliver-a-lilliput
Deux blocs glissent sans frottement sur le sol.
La ligne est infinie vers la droite. A gauche un mur.
Au départ, le bloc de gauche est immobile, celui de droite
a une vitesse de une unité et glisse vers la gauche à
la rencontre de l'autre bloc.
La situation est utopique : on considère que les chocs sont
parfaitement élastiques sans déperdition d'énergie.
Par exemple avec deux masses d'une unité, le bloc de droite
transmet toute son énergie à l'autre lors de la première
collision.
Ensuite le bloc de gauche rebondit sur le mur de gauche, inverse sa
vitesse et transmet toute son énergie à celui de droite
qui va glisser indéfiniment vers la droite avec la vitesse
de une unité (l'opposée de sa vitesse de départ)
sans plus jamais toucher l'autre bloc.
- Expérimenter avec l'animation ci-dessous et observer le nombre
de collisions pour une masse du bloc de droite de 1, 10,
100
puis
16, 32, 64, 81, 90, 102, 400, 103, 104
... 10k, 100n.
Quel
sera le nombre de collisions pour une masse quelconque ?
Quel nombre mystérieux,
le nombre de collisions des blocs permet-il de calculer aussi précisément
que désiré ?

ANIMATION
- Choisir la masse du gros bloc.
- Choisir .le mode animé ou bien
.le mode ultra rapide : compte les collisions sans les simuler en
temps réel.
(utile pour les grandes masses
et automatique dès que le bloc de droite est très loin.
- Lancer avec le bouton GO.
-A tout instant on peut stopper et relancer l'animation.
Le bouton RAZ, réinitialise le tout.
Normalement cela se passe sans bruit.
Cependant un clic dans l'animation permet de mieux repérer
chaque collision et de faciliter le décompte du nombre de collisions.
Pour des raisons pratiques, seules 3 décimales des vitesses
sont affichées.
CLIQUER 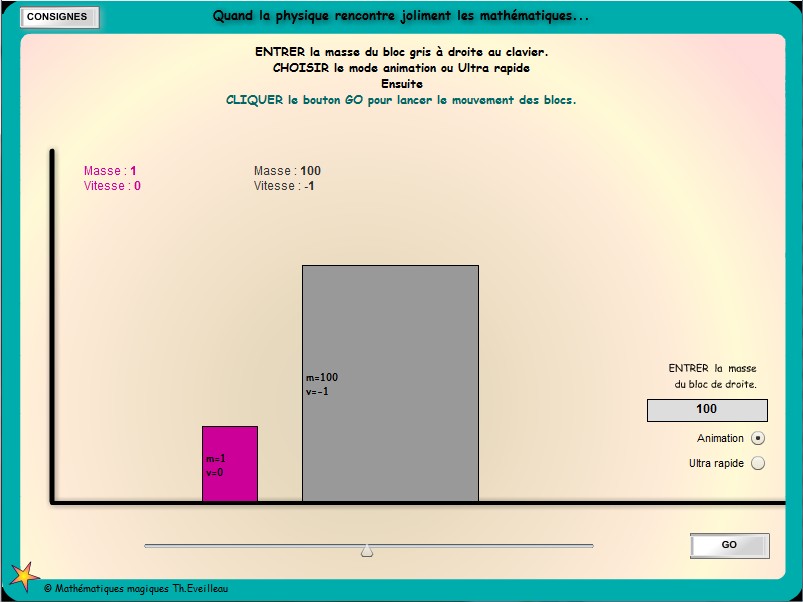

RÉPONSES
et EXPLICATIONS
Pour m=1, nous avons 3 collisions.
Pour m=10, nous avons 10 collisions.
Pour m=100, nous avons 31 collisions.
Et puis
16, 32, 64, 81, 90, 100, 400,
Pour m=16 = 4² , nous avons 12 collisions.
Pour m=32, nous avons 17 collisions.
Pour m=64 = 8² , nous avons 25 collisions.
Pour m=81 = 9² , nous avons 28 collisions.
Pour m=90 , nous avons 29 collisions.
Pour m=400 = 20² , nous avons 62 collisions.
Pour m=10 000 = 100² , nous avons 314 collisions (soit 3.14*100
; 2 décimales de π
sont utilisées).
Pour m=1000 000 = 1003 , nous avons 3141 collisions (soit
3.141*1000 ; 3 décimales de π
sont utilisées).
Pour m=10000 0000 = = 1004 , nous avons 31415 collisions
(soit 3.1415*10000 ; 4 décimales de π
sont utilisées).
Pour les puissances successives
de 100, nous obtenons donc petit à petit les décimales
du nombre π.
Donc en prenant l'unité 1, comme masse du petit bloc et m celle
du gros bloc, le nombre de collisions est  .
.
Ainsi
pour m = 102n = 100n,
nous obtenons π * 10n collisions, c'est-à-dire
que le nombre de collisions donne n décimales précises
du nombre π.
Quand n tend vers l'infini, avec m
= 102n = 100n
si N est le nombre de collisions ALORS
N/ tend vers π.
tend vers π.
De
façon générale pour une masse m du bloc de droite
et une masse de 1 pour celui de gauche,
nous avons un nombre de collisions égal au produit du nombre
π
par la racine carrée du rapport des masses des deux blocs.
Et dans le cas général avec deux blocs de masses m1
(gros bloc) et m2 (petit bloc) , nous obtenons
: 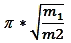 .
.

PREMIÈRE
explication scientifique
Evidemment la magie du résultat a son explication scientifique
qui n'est toutefois pas si simple.
La physique rencontre ici très
joliment les mathématiques.
Pour ceux qui sont effrayés par les explications mathématiques,
il est possible d'observer simplement les animations
du paragraphe suivant avec les rayons lumineux.
Nommons m1 et m2 les masses
des deux blocs, et v1 puis v2
leur vitesse respective positive vers la droite, négative vers
la gauche.
Le gros bloc a l'indice 1, l'autre a l'indice 2.
Le principe repose sur deux propriétés physiques lors
du choc des deux blocs :
- la conservation de l'énergie dont l'équation est :
1/2 m2 * v2² + 1/2
m1* v1² = constanteE.
- la conservation du moment : m2 * v2
+ m1* v1 = constanteM.
Dans le cas présenté au départ nous avons :
constanteE = 1/2 * m2 * 0² + 1/2 * m1
* (-1)² = 0.5*m1
constanteM = m2 * 0 + m1
* (-1) = -m1
En choisissant m2 = 100, nous avons au départ
: constanteE = 50 ET
constanteM = -100
Après le premier choc, le bloc de gauche récupère
une vitesse non nulle et négative.
Les deux équations associées permettent d'obtenir les
vitesses de
v1 = -0.9801980198019803
ET v2 = -1.9801980198019802
Ensuite, lorsque le petit bloc de gauche, rebondit sur le mur, sa
vitesse change simplement de sens. La constante du moment va changer,
mais celle de l'énergie n'est pas modifiée.
N'oublions pas que nous sommes perfectionnistes et
avons supposé des chocs parfaitement élastiques et qu'il
n'y a aucune déperdition d'anergie lors des chocs. Evidemment
c'est une légère entorse à la réalité.
On obtient v2 = 1.9801980198019802
On recalcule alors le moment qui a changé au moment du choc
sur le mur (il reste constant seulement lors du choc des deux blocs)
:
constanteM = -96.03960396039605
L'énergie ne change pas :
constanteE = 50
De là, on recalcule les vitesses : v1
= -0.9215763160474464 ET
v2 = -3.8819723556514063
etc.
Par ailleurs la conservation de l'énergie demeure lors du choc
sur le mur.
Pour
retrouver le nombre π
qui dans notre
esprit est associé à un cercle,
l'idée est de représenter les vitesses sur deux axes
(Ox) et (Oy) en posant
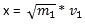 ET
ET 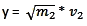
Avec l'équation de conservation de l'énergie
cela donnera l'équation d'un cercle : x² + y² = 2
* ConstanteE.
Utiliser
ensuite la conservation du moment lors du choc entre les
deux blocs.
m2 * v2 + m1
* v1 = constanteM.
Avec les variables x et y, il vient :
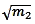 *
*
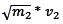 +
+ 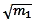 *
*
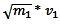 = constanteM
= constanteM
SOIT
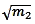 *
y +
*
y + 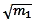 *
x = constanteM.
*
x = constanteM.
Ceci est l'équation d'une droite de pente constante proportionnelle
au rapport : 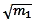 /
/ 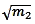 .
.
On
est amené à utiliser des segments de droite,
tous parallèles, car leur pente est constante.
Voici pourquoi ce qui nous intéresse dans le résultat
est essentiellement le rapport des racines
carrées des masses des deux blocs.
Ensuite on utilise les propriétés des angles
inscrits dans un cercle et on arrivera au résultat.
...
Pour retrouver l'explication complète (relevant toutefois
d'un bon niveau en mathématiques),
voir le lien externe qui suit (en anglais).
|
|
C'est excellent
: https://www.youtube.com/watch?v=jsYwFizhncE&feature=youtu.be
Il y a aussi celle-ci toujours en anglais:
https://clairelommeblog.wordpress.com/2014/08/31/pi-passe-sur-le-billard/
Le processus
est assez long pour obtenir de nombreuses décimales du nombre
π
et au bout du compte si c'est très joli, ce
n'est pas très efficace.

CHANGEMENT
de POINT de vue
Collisions
sur une droite
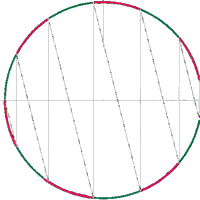
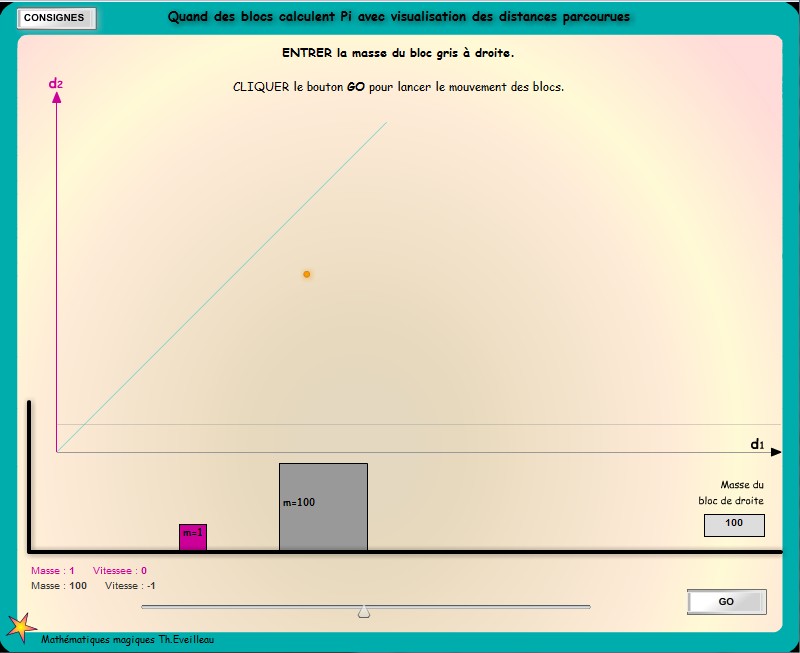
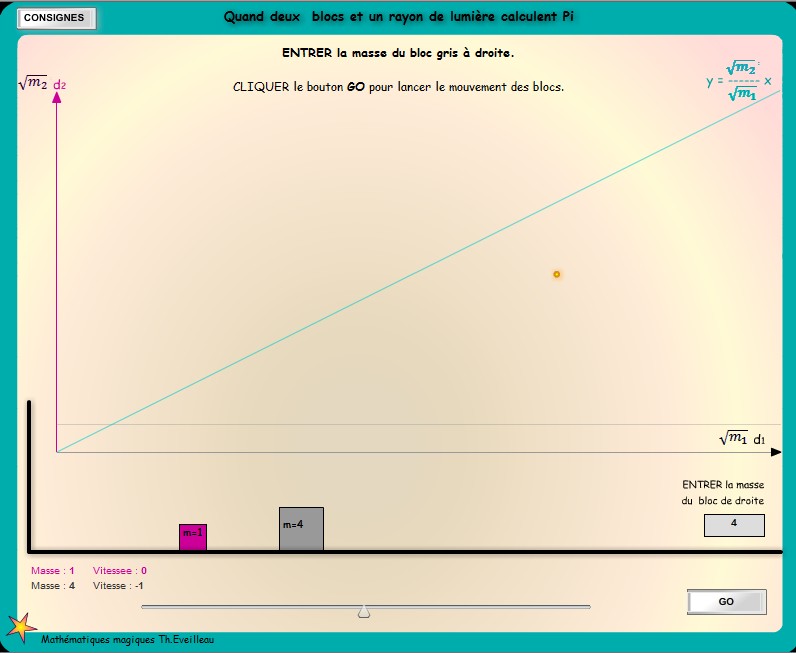
Nous représentons maintenant sur un graphique les distances
parcourues par les deux blocs.
Sur l'axe des abscisses nous notons la distance
d1 parcourue par le bord gauche du gros bloc
gris.
Sur l'axe des ordonnées nous notons
la distance d2
parcourue par le bord droit du petit bloc rouge.
Le gros point jaune a pour coordonnées les distances d1
et d2, parcourues par les deux blocs.
Nous traçons en vert, la bissectrice
de l'angle des deux axes, a pour équation y = x, c'est-à-dire
d1 = d2.
Ainsi,
- chaque intersection des courbes(x,y) avec cette oblique représente
une collision des deux blocs,
puisqu'alors on a égalité des distances d1
et d2 des deux blocs ;
- chaque intersection des courbes(x,y) avec l'axe (Ox) représente
un rebond du bloc rouge contre le mur,
puisqu'alors la distance d2 s'annule et que
la vitesse v2 change simplement de sens.
Le nombre de collisions des deux blocs, devient
le nombre d'intersections des trajets avec l'axe des abscisses et
avec l'oblique.
CLIQUER
Pour
l'instant
- l'axe des abscisses peut
être considéré comme un miroir. L'angle d'incidence
du rayon est égal à l'angle de réflexion.
En effet, lors du rebond sur le mur,
. la vitesse du bloc gris
reste inchangée,
. celle du bloc rouge, change
simplement de sens, mais sa valeur absolue reste identique (n'oublions
pas que nous sommes dans une situation idéale où il
n'y a pas de déperdition d'énergie).
- par contre, ce n'est pas
le cas de la droite verte dans le cas général, puisque
l'angle de réflexion du rayon n'est pas égal au rayon
d'incidence.
Nous allons donc ci-après effectuer quelques modifications
afin d'obtenir l'illusion d'un rayon lumineux se réfléchissant
sur deux miroirs.

Vers
un rayon lumineux
. d1
est toujours la distance parcourue par le bord gauche du gros bloc
gris.
. d2 la
distance parcourue par le bord droit du petit bloc rouge.
Le gros point jaune a cette fois pour coordonnées
->
x = 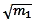 *d1
sur l'axe des abscisses puis
*d1
sur l'axe des abscisses puis
->
y = 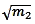 *d2
sur l'axe des ordonnées.
*d2
sur l'axe des ordonnées.
Nous traçons en vert, la droite d'équation
y = (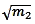 /
/ 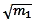 ) * x,.
) * x,.
CLIQUER
Lorsque
y = (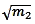 /
/ 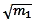 ) * x,
avec
y =
) * x,
avec
y = 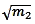 *d2
ET
x =
*d2
ET
x = 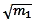 *d1,
*d1,
nous obtenons :
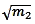 *d2
= (
*d2
= (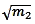 /
/ 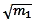 ) *
) *
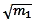 *d1
*d1
c'est-à-dire
d1 = d2.
Ainsi nous avons toujours :
- chaque intersection des courbes(x,y) avec cette oblique représente
une collision des deux blocs,
- chaque intersection des courbes(x,y) avec l'axe (Ox) représente
un rebond du bloc rouge contre le mur.
Le nombre de collisions des deux blocs, est toujours le nombre d'intersections
des trajets avec l'axe des abscisses et avec l'oblique.
Cette fois, lorsque le 'rayon' arrive sur la droite oblique, l'angle
de réflexion est égal à l'angle d'incidence
(Cf démonstration ci-dessous).
La droite verte et l'axe des abscisses et peuvent être considérés
comme deux miroirs sur lesquels le 'rayon lumineux' se réfléchit.
Le
problème du nombre de collisions des deux blocs se ramène
donc au problème du nombre de réflexions arrivant
sur deux miroirs faisant entre eux un angle variable.
Retrouvez
ce problème animé et résolu lumineusement en
changeant encore de point de vue
ICI :
Réflexion d'un rayon lumineux entre deux miroirs.

DÉMONSTRATION
de l'égalité de l'angle de réflexion et de
l'angle d'incidence
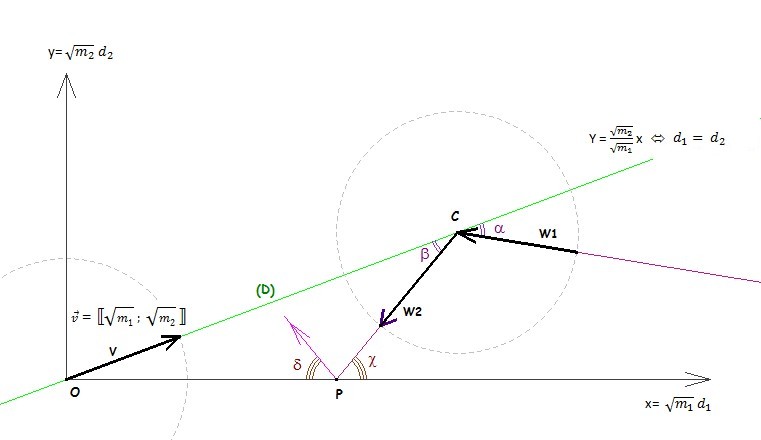
Choisissons comme composantes du vecteur V
directeur de la droite verte :  ET
ET  .
.
Après la collision des deux blocs, traduite par le point
C sur la droite oblique, les vitesses v1
ET
v2 deviennent
v'1
ET
v'2 .
Définissons les deux vecteurs W1 et
W2 par leurs composantes :
-
vecteur W1 sont : dx/dt
=  v1
ET dy/dt
=
v1
ET dy/dt
= 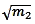 v2.
v2.
-
vecteur W2 sont : dx/dt
= 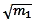 v'1
ET dy/dt
=
v'1
ET dy/dt
= 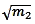 v'2.
v'2.
Ces vitesses
vérifient l'équation de conservation de l'énergie
: 0.5
* m2 * v2²
+ 0.5 * m1* v1²
= constanteE .
Cette équation peut s'écrire :
m2
* v2² + m1
* v1²
= 2*constanteE
OU
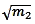 *
*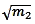 * v2² +
* v2² + 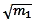 *
*
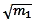 * v1²
= 2*constanteE
OU
* v1²
= 2*constanteE
OU
(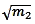 * v2 )² + (
* v2 )² + (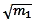 * v1
) ²
= 2*constanteE
OU
* v1
) ²
= 2*constanteE
OU
||W1|| ² = 2*constanteE
De mêm nous aurions : ||W2||
² = 2*constanteE
Cette dernière ligne signifie que la longueur, du vecteur
W1 , obtenue avec la distance euclidienne,
(sa norme) est de valeur constante.
Nous avons le même résultat pour le vecteur W2.
Les deux vecteurs W1
et W2 ont donc la
même norme : ||W1||
= ||W2||
Utilisons maintenant la propriété
de conservation des moments
m2
* v2 + m1* v1
= constanteM
qui s'écrit
également : 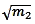 *
* 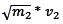 +
+ 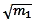 *
* 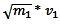 = constanteM.
= constanteM.
OR
cette dernière équation traduit le produit scalaire
du vecteur W1 par
le vecteur directeur V, de la droite d'équation
y = (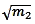 /
/ 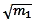 ) * x :
) * x :
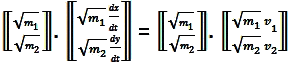
Nous avons le même résultat avec le le produit scalaire
du vecteur W2 par
le vecteur directeur V :

Nous avons l'égalité des produits scalaires des vecteurs
: W1 . V = W2
. V
Utilisons maintenant le produit scalaire comme, produit des normes
des deux vecteurs par le cosinus de l'angle qu'ils fotn entre eux.
Nous obtenons :
||W1|| * ||V|| *
cos(α)= ||W2||
* ||V|| * cos(β)
Et comme
||W1||
= ||W2||,
nous déduisons
qu'au signe près les angles α et β sont de même
mesure.
Avant et après la collision des deux blocs en le point C,
les angles sont de même mesure.
Ils
peuvent être assimilés à un angle d'incidence
et de réflexion d'un rayon lumineux.
Pour
ce qui est des deux angles en P, sur la droite horizontale, l'égalité
des mesures des angles est évidente, puisque la vitesse du
petit bloc rouge qui rebondit sur le mur, change seulement de sens
en gardant la même valeur absolue.
Il y a symétrie de la situation et les deux angles sont de
même mesure.
On peut
donc changer de point de vue et penser la situation de collision
des deux blocs comme la réflexion d'un rayon lumineux sur
deux miroirs faisant un angle θ, dont la tangente est le rapport
des masses des deux blocs.
Y-a-t-il
CONTRADICTION ?
Nous avons trouvé un peu plus haut que le nombre de collisions
est la partie entière de : 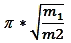 .
.
Avec les miroirs,
si θ (en radians) et est l'angle dont la tangente est : 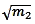 /
/ 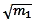 ,
,
nous trouvons que le nombre de réflexions est
( aux approximations avec la partie entière près)
:
E(π / θ ) .
θ
est donc l'angle dont la cotangente est 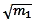 /
/ 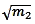 .
.
NON, pas de contradiction,
car dans le problème qui nous intéresse, le rapport
entre m1 et m2 est assez
grand et l'angle θ
est
petit, la formule de Taylor, permet d'écrire :
tan x = x + x3/3 + 2x5/15 + 17x7/315
+ ... pour | x | < π/2
On pourra assimiler tan x ~ x
π
/θ
devient
π
/ tan θ
SOIT
π
/ (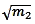 /
/ 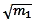 )
)
qui finalement permet de retrouver : 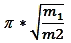 .
.
C.Q.F.D
π
est irrationnel MAIS bien tourné !

AUTRES
expériences autour du
nombre π
Il existe d'autres façons expérimentales ou numériques
beaucoup plus rapides de retrouver les décimales du nombre
π.
En voici trois exemples dans ce site :
- Archimède
il y a bien longtemps... ICI.
-
Les aiguilles de Buffon
ICI.
- La méthode de
Monte-Carlo ICI.
Par ailleurs le nombre π
se calcule
avec la limite
de nombreuses séries numériques convergeant plus ou
moins rapidement.
Cependant dans ces méthodes, le résultat est de nature
probabibiliste. On ne peut pas garantir une précision spécifique.
PAR
CONTRE,
avec la méthode précédente
dite du billard, idéalisée en prenant des chocs complètement
élastiques, sans déperdition d'énergie, c'est
différent.
La méthode est déterministe : on est CERTAIN de pouvoir
obtenir le nombre désiré de décimales de π.
Bien sûr ce peut être long mais c'est certain. Il n'y
a pas de hasard.
Il
suffit de choisir des blocs dont les masses ont le bon rapport,
c'est-à dire 100n si l'on veut obtenir n décimales
de π.
Un excellent
article (en anglais) de G.GALPERIN ICI

Petite
question subsidiaire pour se détendre
:
-Quel est le lien entre le 14 mars et le 27 juillet ? (1)


 .
.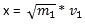 ET
ET