Approximations rationnelles de la racine carrée de deux

Euclide il y a environ 2500 ans...
" Figure-toi un carré de côté mesurant l’unité dont on considérerait une diagonale...
Ne te semblerait-t-il pas naturel que cette diagonale ait une longueur ?
Ne dirais-tu pas que cette longueur est égale à une quantité entière ou fractionnelle ?
Et si celle-ci n’était pas entière, ne penserais-tu pas qu’elle ne pourrait être autre que fractionnaire ?
Et si je t’affirmais le contraire, ne me dirais-tu pas que je suis frappé d’hérésie ? "

MESURER avec une unité arbitraire

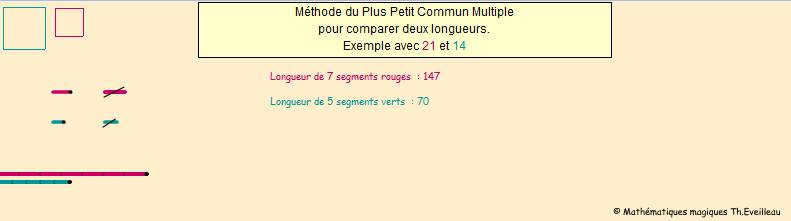
La méthode du Plus Petit Commun Multiple
Par exemple, prenons le segment rouge (qui mesure en réalité 21 pixels) et le segment vert (qui mesure 14 pixels).
Bien entendu, nous ne nous servirons pas de ces indications.
Nous trouvons une longueur commune en reportant trois segments rouges puis trois segments verts.
Ainsi un segment rouge vaut 3/2 segment vert.
En poursuivant la duplication, nous trouverons d'autres fractions équivalentes.

Sur l'animation suivante, dupliquer tour à tour, en cliquant dessus, les traits rouge et vert sur la gauche.
Il faut obtenir des longueurs rouge et verte égales.

Les traits rouge et vert, barrés permettent d'effacer des segments.

Sur le même principe on peut comparer une aire A avec une aire B choisie arbitrairement. Il suffit de superposer deux pavages, l'un obtenu avec A et l'autre avec B.
De même on peut mesurer la capacité d'un récipient A avec celle d'un récipient B...
Et pourquoi pas procéder de la même façon avec des unités de masse voire de temps...

(1) La méthode du Plus Grand Commun Diviseur (PGCD) permet d'obtenir des résultats similaires en soustrayant la petite unité de la grande plusieurs fois de suite.

-Le point de rencontre existe-t-il toujours ?
-Physiquement, on peut décider d'une certaine précision.
-Mais mathématiquement le point de rencontre existe-t-il toujours ?

Prenons l'exemple de la diagonale d'un carré de côté de longueur une unité

Cette diagonale mesure

On aligne les segments rouges de longueur L (en l'occurrence ici, la racine carrée de deux) avec des segments unité U afin d'obtenir une longueur commune avec une certaine précision.
On peut aussi s'exercer avec une feuille A4 : trouver une longueur commune entre la longueur et la largeur de la feuille (en effet le rapport longueur sur largeur d'une feuille A4 est

). Voir les différents formats A, B...

Ayant construit une longueur presque commune, par exemple
5 L ~ 7 U alors nous notons que
la mesure de L est environ (7 / 5) U

Sur l'animation suivante, dupliquer tour à tour, en cliquant dessus, les traits rouge et vert sur la gauche.
Essayer d'obtenir des longueurs rouge et verte sensiblement égales.
Alors une approximation rationnelle de la racine carrée de 2 sera affichée avec la précision obtenue.

Il est impossible d'obtenir une longueur parfaitement commune car est irrationnel.

DÉMONTRONS par l'absurde qu'il n'existe aucune fraction irréductible égale à .

Supposons qu'il existe deux entiers a et b tels que la fraction 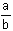soit irréductible et que = .
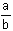Nous avons a² = 2b².
cette fraction étant irréductible, il n'y a que trois cas possibles car a et b ne peuvent pas être tous les deux pairs :

1°) a est impair et b est impair, leurs carrés a² et b² sont impairs tous les deux.
Et
2b² est pair, a² est impair ET a² = 2b²
Ceci aboutit à l'égalité entre un nombre pair et un nombre impair.
C'est impossible !

2°) a est impair et b est pair, a² est impair et 2b² est pair.
Comme ci-dessus c'est impossible !

3°) a est pair et b est impair,
a² est pair et multiple de 4
et 2b² est pair mais non multiple de 4 car b est impair.
Il est donc impossible que a² = 2b².

Nous avons démontré qu'il est impossible de trouver une fraction irréductible égale à la racine carrée de deux.

Chez les BABYLONIENS

Les Babyloniens obtenaient un encadrement de la racine , en consultant une table de carrés.
Ils notaient (1 ; 25) la valeur : .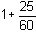
Ils connaissaient également la valeur plus précise : 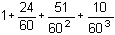qu'ils notaient (1 ; 24 ; 51 ; 10 ).

D'autres fractions pour la racine carrée de 2

Nous savons que la racine carrée de 2 est solution de l'équation :
x² = 2. Cela s'écrit x² - 1 = 1 ou encore (x - 1) (x + 1) = 1
d'où

L'animation, suivante permet de voir l'évolution des approximations selon la valeur de a et le rang du calcul.
Avec F5 on a déjà une très bonne approximation de

CLIQUER