Eléments d'Euclide

A l'époque d'Alexandre le Grand vers -350 avant notre ère, les bords du Nil étaient annuellement fertilisés par les inondations du fleuve. Les agriculteurs devaient retrouver les limites de leurs terres ou du moins retrouver une parcelle d'une superficie équivalente, car le fleuve nourricier détruisait tous les repères. Cette tâche était confiée à des gens qui "mesuraient la terre" : des GEOMETRES (du grec géo pour la terre et metron, mesure). Alexandrie possédait alors la plus grande bibliothèque de l'Antiquité. Le plus grand des mathématiciens vivant à Alexandrie, s'appelait Euclide. Il écrivit le premier ouvrage de Géométrie dont on a gardé les traces : les Eléments d'Euclide. Cet ouvrage comporte 13 livres. On retrouve dans les deux premiers des règles de démonstration qui permettent de dérouler des suites de théorèmes logiquement reliés les uns aux autres. Mais les mathématiciens d'Alexandrie ne se sont pas satisfaits pas de la résolution de ces partages de terres. Ils déroulèrent leur raisonnement hors du domaine pratique, comme un jeu de l'esprit soumis à de nouvelles règles : celles de la logique.

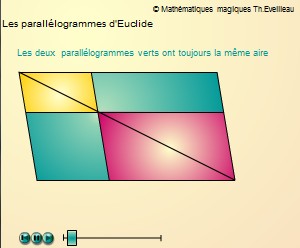
Parallélogrammes équivalents
Le théorème suivant est extrait des Eléments dans le livre I, proposition 43.

Prenons un rectangle. Par un point quelconque de sa diagonale traçons les parallèles à ses côtés.

Les deux rectangles verts de chaque côté de la diagonale ont la même aire.

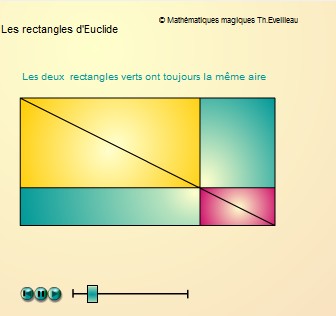Le résultat est identique avec des parallélogrammes au lieu de rectangles.

Par un point quelconque de la diagonale d'un parallélogramme traçons les parallèles à ses côtés.

Les deux parallélogrammes de chaque côté de la diagonale ont la même aire.

Résumé
De chaque côté de la diagonale d'un rectangle ou d'un parallélogramme on a deux surfaces de même aire par symétrie centrale. A chacune on a enlevé deux morceaux de forme triangulaire. Or ces morceaux sont superposables de chaque côté. Ceux qui restent ont donc même aire.
La beauté de la démonstration réside dans sa simplicité !