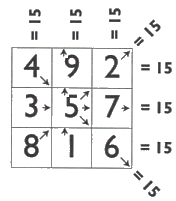|
Merveilleux
carrés
magiques...
Boutons des animations
Les
flèches simples permettent d'avancer ou de reculer pas à
pas à chaque clic.
La
double flèche avant permet une lecture automatique.
La
double flèche arrière revient au début.
 Définition Définition
Un
carré magique d'ordre n est un tableau carré, formé
de cases en même nombre dans les lignes et les colonnes.
Dans chaque case est écrit un nombre, de telle sorte que les
n2 premiers entiers soient écrits,
que les sommes des nombres pris dans une même ligne, une même
colonne,
ou dans chacune des deux diagonales, soient égales.
 Exemple
avec un carré de 3 cases de côté Exemple
avec un carré de 3 cases de côté
Il s'agit de
placer les nombres de 1 à 9, de telle façon que la somme
des nombres sur chacune des 3 lignes,
chacune des 3 colonnes et chacune des deux diagonales soit la même.
Plusieurs questions
se posent :
Cette somme peut-elle varier ?
La solution est-elle unique ?
La somme est unique :
En effet on utilise tous les nombres de 1 à 9 dont la somme
est égale à 45 (Cf le gnomon
dans ma Trucs Maths).
Les 3 lignes ont la même somme, donc sur chaque ligne, la
somme est de 45/3,
soit 15. Il en est de même pour chaque colonne.
Si l'on décompose 15 en somme de 3 nombres différents
allant de 1 à 9, on trouve 8 possiblités :
1 + 5 + 9
1
+ 6 + 8
2
+ 4 + 9
2
+ 5 + 8
2 + 6 + 7
3
+ 4 + 8
3
+ 5 + 7
4
+ 5 + 6
On note que dans ces décompositions, le nombre 5 apparaît
4 fois, il est situé au centre du carré et
il interviendra dans une ligne, une colonne et les deux diagonales.
Le nombre 2 (tout comme le 4, le 8 et le 6), apparaît
3 fois, il est donc situé dans un coin du carré
pour intervenir dans une ligne, une colonne et une diagonale.
Le nombre 9 (tout comme le 3, le 7, et le 1), apparaît
2 fois, il est donc situé au milieu d'une ligne ou
d'une colonne d'un bord pour intervenir une fois dans une ligne
et dans une colonne.
La solution
n'est pas unique :
Les résultats précédents montrent que la solution
est unique à des rotations et symétries près.
On trouve finalement 8 configurations du carré magique d'ordre
3, en voici une ci-dessous.
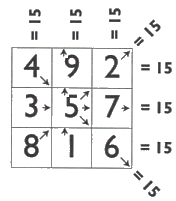

 Calcul
de la somme magique Calcul
de la somme magique
Lorsque
nous avons un carré de n cases sur n cases de côté,
nous utilisons les n2 premiers
nombres entiers dont la somme est
n2 (n2+1)/2
(Cf le gnomon
dans
ma page Trucs Maths).
Les n lignes ont chacune
la même somme qui est donc égale au résultat précédent
divisé par n soit à n(n2+1)/2.
Par exemple si n = 4, la somme magique est 4(16+1)/2 soit 4(17)/2 soit
34.
Le carré de la Sagrada Familia
Sur la Sagrada Familia
de Barcelone Josep Maria Subirachs a sculpté a façade
de la Passion de la Basilique.
On y découvre juste à côté du baiser de Judas,
un carré magique gravé dans la pierre.
| Le
carré magique de la Sagrada Familia

|
| 1 |
14 |
14 |
4 |
| 11 |
7 |
6 |
9 |
| 8 |
10 |
10 |
5 |
| 13 |
2 |
3 |
15 |
La
somme magique
de ce carré est 33.
|
|
Cette somme magique n'est pas 34
comme dans le carré classique suivant.
| 1 |
12 |
8 |
13 |
| 6 |
15 |
3 |
10 |
| 11 |
2 |
14 |
7 |
| 16 |
5 |
9 |
4 |
|
| La
somme 33 se retrouve également
sur les carrés intérieurs.
CLIQUER
|
Il
semblerait que Subirachs soit parti du célèbre
carré magique
de la Mélancolie de Dürer
à un demi-tour près,
dans lequel il a retranché 1 aux quatre nombres
15, 12, 11 et 16.
Il y a de nombreuses façons de retrouver ce carré
à des symétries et rotations près.
Dürer aurait pu graver 32 carrés magiques avec la
même position de la date 1514.
Et... il existe 880 carrés
magiques normaux d'ordre 4, utilisant les nombres de 1 à
16.
CF les liens internes :
car_mag5.htm#sept
et
B132.pdf
|
| Ci-dessous,
le carré magique
de la Mélancolie de Dürer :
| 16
|
3 |
2 |
13 |
| 5 |
10 |
11 |
8 |
| 9 |
6 |
7 |
12 |
| 4 |
15 |
14 |
1 |
|
Le
carré de la Mélancolie avec une rotation d'un demi-tour
autour de son centre :
| 1 |
14 |
15 |
4 |
| 12 |
7 |
6 |
9 |
| 8 |
11 |
10 |
5 |
| 13 |
2 |
3 |
16 |
|
On
retranche 1 aux quatre nombres 15,12, 11 et 16 ==> le
carré de la Sagrada Familia.
| 1 |
14 |
14 |
4 |
| 11 |
7 |
6 |
9 |
| 8 |
10 |
10 |
5 |
| 13 |
2 |
3 |
15 |
|
La présence de ce carré
sur la façade d’une église paraît insolite.
Il est appelé le cryptogramme de Subirachs.
Dans un carré magique normal, nous n'utilisons qu'une et une
seule fois chaque nombre du carré.
Dans celui de la Sagrada Familia il y a répétition des
deux nombres 10 et 14.
Les interprétations des nombres utilisés dans ce carré
sont diverses.
- Il semblerait que la somme magique 33, soit
en relation avec l’âge présumé de la mort
du Christ : 33 ans.
Ce même nombre apparaît aussi dans le Parc Guëll
pour la somme des escaliers.
-Certains pensent que le secret du carré serait à rechercher
dans la franc-maçonnerie du rite écossais ancien et accepté
qui comporte 33 degrés
(les 3 premiers grades symboliques correspondant aux loges dites
« bleues » auxquels viennent s’ajouter des grades
complémentaires dits « hauts grades »).
- Le nombre 12 n’apparaît pas,
contredisant ainsi les règles mathématiques du carré.
L’une des explications avancées serait que ce nombre
12 aurait été intentionnellement occulté pour nier
l’existence des 12 apôtres.
Mais cela reste un mystère que Subirachs a emporté
avec lui dans sa tombe.
Remarque
En
utilisant les premiers entiers de 0 à 16, sans le nombre 4 par
exemple, , nous pouvons obtenir un carré magique d'ordre 4, de
somme 33 au lieu de 34 et ce sans répétition de nombre.
En
voici un exemple :
| 0 |
5 |
12 |
16 |
| 15 |
11 |
6 |
1 |
| 10 |
3 |
13 |
7 |
| 8 |
14 |
2 |
9 |
Secret
de magie (http://www.youtube.com/embed/MZzzH9voyAI
)
Si l'on connaît par cœur le carré magique ci-dessous, on
peut épater les amis en en trouvant rapidement d'autres,
ayant une somme arbitraire supérieure à 34.
En effet, dans ce carré, on note que les 4 premiers nombres 1,
2, 3 et 4 sont situés sur 4 lignes et 4 colonnes différentes.
Aussi pour atteindre sur chaque ligne, chaque colonne etc, la somme
désirée,
il suffit seulement d'ajouter aux quatre premiers nombres de 1 à
4, le complément de 34 à la somme désirée.
|
1
|
16
|
10
|
7
|
|
6
|
11
|
13
|
4
|
|
15
|
2
|
8
|
9
|
|
12
|
5
|
3
|
14
|
Par exemple si l'on
veut une somme de 56, il suffit d'ajouter 22 = 56 - 34 à
chacun des quatre nombres 1, 2, 3 et 4.
Ainsi on remplace
1 par 1+ 22 soit 23 puis
2 par 24, puis
3 par 25 et enfin
4 par 26.
Les autres nombres restent inchangés.
|
23
|
16
|
10
|
7
|
|
6
|
11
|
13
|
26
|
|
15
|
24
|
8
|
9
|
|
12
|
5
|
25
|
14
|
On obtient un carré
magique dont la somme est 56.
Ce carré possède de nombreuses propriétés
de symétrie.
Applaudissez
maintenant le magicien belge dans la vidéo suivante :
http://www.youtube.com/embed/MZzzH9voyAI
VARIANTE
De même dans la vidéo suivante,
http://www.dailymotion.com/video/xs3j7q_gili-le-carre-magique_fun?search_algo=1
,
le même
excellent magicien part du carré magique de somme 54 (aux
nombreuses propriétés de symétrie)
constitué des entiers consécutifs de 6 à 21 :
|
6
|
11
|
20
|
17
|
|
21
|
16
|
7
|
10
|
|
15
|
18
|
13
|
8
|
|
12
|
9
|
14
|
19
|
Il suffit par exemple
de remplacer les quatre premiers nombres 6, 7, 8 et 9 par
6 + 23 = 29
7 + 23 = 30
8 +23 = 31 et enfin
9 + 23 = 32.
Pourquoi 23 ?
Parce que la différence, entre le nombre proposé par le spectateur
: 77 et la somme magique 54,
est 77 - 54 = 23.
Ainsi on constitue un nouveau carré magique de somme 77.
|
29
|
11
|
20
|
17
|
|
21
|
16
|
30
|
10
|
|
15
|
18
|
13
|
31
|
|
12
|
32
|
14
|
19
|
Pour fabriquer rapidement ce carré en tenant compte du nombre
proposé par le spectateur, il suffit de
- mémoriser le premier carré magique des entiers de 6 à 21 et
- soustraire 54 au nombre proposé par le spectateur.
Ce nombre peut être négatif car le spectateur choisit un
nombre entre 51 et 99 :
avec 52 on aurait 52 - 54 = -2.
- modifier les quatre nombres de 6 à 9 en leur ajoutant le résultat
de la soustraction, en tenant surtout compte du signe du résultat.
Exemple
Si le spectateur propose 52, le résultat de la soustraction est
52 - 54 = -2
donc effectuer :
6 - 2 = 4 puis
7 - 2 = 5 puis
8 - 2 = 6 et enfin
9 - 2 = 7.
Voici la grille avec la somme 52 :
|
4
|
11
|
20
|
17
|
|
21
|
16
|
5
|
10
|
|
15
|
18
|
13
|
6
|
|
12
|
7
|
14
|
19
|
Entrer la somme désirée
avec les flèches ou au clavier (suivi de ENTREE).
On peut obtenir des carrés variés avec la même somme.
CLIQUER



|